练习册

  • 练习册
  • 试题
    相关习题
     0  47301  47309  47315  47319  47325  47327  47331  47337  47339  47345  47351  47355  47357  47361  47367  47369  47375  47379  47381  47385  47387  47391  47393  47395  47396  47397  47399  47400  47401  47403  47405  47409  47411  47415  47417  47421  47427  47429  47435  47439  47441  47445  47451  47457  47459  47465  47469  47471  47477  47481  47487  47495  266669 

    科目： 来源： 题型：

    （2012•北京模拟）甲、乙、丙、丁四个人进行传球练习，每次球从一个人的手中传入其余三个人中的任意一个人的手中．如果由甲开始作第1次传球，经过n次传球后，球仍在甲手中的所有不同的传球种数共有an种．
    （如，第一次传球模型分析得a1=0．）
    （1）求 a2，a3的值；
    （2）写出 an+1与 an的关系式（不必证明），并求 an=f（n）的解析式；
    （3）求 
    anan+1
    的最大值．

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•北京模拟）在数列{an}中，a1=
    		3
    ，an+1=
    		1+
    a
    2
    n
    -1
    an
    (n∈N*)    ．数列{bn}满足0＜bn＜
    π
    2
    ，且 an=tanbn（n∈N*）．
    （1）求b1，b2的值；
    （2）求数列{bn}的通项公式；
    （3）设数列{bn}的前n项和为Sn．若对于任意的n∈N*，不等式Sn≥(-1)nλbn恒成立，求实数λ的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

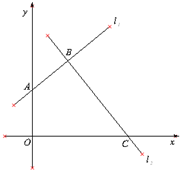    （2012•北京模拟）如图，经过B（1，2）作两条互相垂直的直线l1和l2，l1交y轴正半轴于点A，l2交x轴正半轴于点C．
    （1）若A（0，1），求点C的坐标；
    （2）试问是否总存在经过O，A，B，C四点的圆？若存在，求出半径最小的圆的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•北京模拟）设等差数列{an}的前n项和为Sn，且Sn=(
    an+12
    )2    ，（n∈N*），若bn=(-1)nSn，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•北京模拟）在△ABC中，a，b，c分别是角A，B，C的对边，若三边长a，b，c依次成等差数列，sinA：sinB=3：5，求三个内角中最大角的度数．

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•北京模拟）平面上画了一些彼此相距2a的平行线，把一枚半径为r（r＜a）的硬币任意掷在这个平面上，求硬币不与任何一条平行线相碰的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•北京模拟）假设某种设备使用的年限x（年）与所支出的维修费用y（元）有以下统计资料：
    使用年限x 2 3 4 5 6
    维修费用y 2.2 3.8 5.5 6.5 7.0
    参考数据：
    5
    i=1
    xi2=90    ，
    5
    i=1
    xiyi=112.3    ，
    如果由资料知y对x呈线性相关关系．试求：
    （1）
    .
    x
    ，
    .
    y
    ；
    （2）线性回归方程
    ∧
    y
    =bx+a．
    （3）估计使用10年时，维修费用是多少？

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•北京模拟）已知平面上的四个点A、B、C、D，其中A（-2，0），B（2，0），D（x，y），如果|
    AC
    |=2    ，
    AD
    =
    1
    2
    (
    AB
    +
    AC
    )    ．
    求证：x2+y2=1．

    查看答案和解析>>

    科目： 来源： 题型：

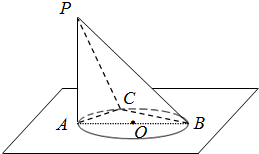    （2012•北京模拟）如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A、B的任意一点．
    （1）求证：BC⊥平面PAC；
    （2）求证：平面PAC⊥平面PBC．

    查看答案和解析>>

    科目： 来源： 题型：

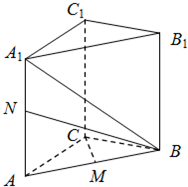    （2012•北京模拟）如图，三棱柱ABC-A1B1C1的侧棱A1A垂直于底面ABC，A1A=2，AC=CB=1，∠BCA=90°，M、N分别是AB、A1A的中点．
    （1）求BN的长；
    （2）求证：A1B⊥CM．

    查看答案和解析>>

    同步练习册答案