
科目: 来源: 题型:

图2-5-20
(1)求△ABC的边AB上的高h.
(2)设DN=x,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85米的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果为保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开大树.
查看答案和解析>>
科目: 来源: 题型:
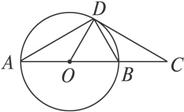
图2-5-19
查看答案和解析>>
科目: 来源: 题型:
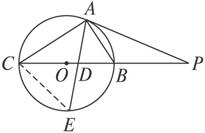
图2-5-18
查看答案和解析>>
科目: 来源: 题型:
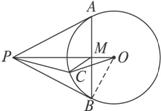
图2-5-16
查看答案和解析>>
科目: 来源: 题型:
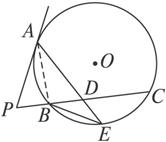
图2-5-15
求证:(1)PA=PD;
(2)BP2=![]() AD·DE.
AD·DE.
查看答案和解析>>
科目: 来源: 题型:
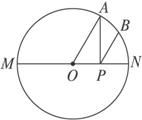
图2-5-12
A.1 B.![]() C.
C.![]() -1 D.
-1 D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com