在极坐标系中.A(4,),B(1,),则△OAB的面积是 .——青夏教育精英家教网—

相关习题

科目： 来源： 题型：

在极坐标系中，A(4,),B(1,),则△OAB的面积是__________.

科目： 来源： 题型：

极坐标与直角坐标的互化：

（1）化点M的直角坐标（-3，4）为极坐标；

（2）化点M的极坐标（-2，）为直角坐标.

科目： 来源： 题型：

设有一颗彗星，围绕地球沿一抛物线轨道运行，地球恰好位于该抛物线轨道的焦点处，当此彗星离地球为30（万千米）时，经过地球和彗星的直线与抛物线的轴的夹角为30°，试建立适当的极坐标系，写出彗星此时的极坐标.

科目： 来源： 题型：

用极坐标与直角坐标来表示点时，二者究竟有哪些相同和不同呢？

科目： 来源： 题型：

平面内建立直角坐标系是人们公认的最容易接受并且被经常采用的方法，但为什么它并不是确定点的位置的唯一方法，为什么要使用极坐标?

科目： 来源： 题型：

如图1-1-7所示，一个椭圆的长轴长为2a，短轴长为2b，在一直角EOF内滚动，并始终与∠EOF的两边OE、OF分别相切.求椭圆中心O′的轨迹.

图1-1-7

科目： 来源： 题型：

某河上有抛物线型拱桥，当水面距拱顶5 m时，水面宽8 m，一木船宽4 m，高2 m，载货后木船露在水面上的部分高为 m，问水面上涨到与抛物线拱顶相距多少米时，木船开始不能通航？

科目： 来源： 题型：

如图1-1-6，某隧道设计为双向四车道，车道总宽22米，要求通行车辆限高4.5米，隧道全长2.5千米，隧道的拱线近似地看成半个椭圆形状.

图1-1-6

（1）若最大拱高h为6米，则隧道设计的拱宽l是多少？

（2）若最大拱高h不小于6米，则应如何设计拱高h和拱宽l，才能使半个椭圆形隧道的土方工程量最小？（半个椭圆的面积公式为S=lh，柱体体积为底面积乘以高.本题结果精确到0.1米）

科目： 来源： 题型：

如图1-1-5，已知A、B、C是直线m上的三点，且|AB|=|BC|=6，⊙O′切直线m于点A，又过B、C作⊙O′异于m的两切线，切点分别为D、E，设两切线交于点P.

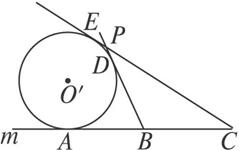
图1-1-5

（1）求点P的轨迹方程;

（2）经过点C的直线l与点P的轨迹交于M、N两点，且点C分所成比等于2∶3，求直线l的方程.

科目： 来源： 题型：

已知△ABC的底边BC长为12，且底边固定，顶点A是动点，sinB-sinC=sinA，求点A的轨迹.

同步练习册答案