
科目: 来源: 题型:

A.2∶1 B.3∶1 C.3∶2 D.4∶3
查看答案和解析>>
科目: 来源: 题型:
A.α、β都垂直于平面γ
B.α内存在不共线三点到β的距离相等
C.l、m是α内两条直线,且l∥β,m∥β
D.l、m是两条异面直线,且l∥α,m∥α,l∥β,m∥β
查看答案和解析>>
科目: 来源: 题型:
①若A⊥b,A⊥α,b![]() α,则b∥α ②若A∥α,α⊥β,则A⊥β ③若A⊥β,α⊥β,则A∥α或A
α,则b∥α ②若A∥α,α⊥β,则A⊥β ③若A⊥β,α⊥β,则A∥α或A![]() α ④若A⊥b,A⊥α,b⊥β,则α⊥β
α ④若A⊥b,A⊥α,b⊥β,则α⊥β
A.0 B.1 C.2 D.3
查看答案和解析>>
科目: 来源: 题型:
①α∥β![]() l⊥M ②α⊥β
l⊥M ②α⊥β![]() l∥M
l∥M
③l∥M![]() α⊥β ④l⊥M
α⊥β ④l⊥M![]() α∥β
α∥β
A.①② B.③④ C.②④ D.①③
查看答案和解析>>
科目: 来源: 题型:
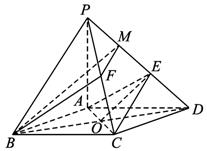
(1)证明PA⊥平面ABCD.
(2)求以AC为棱,EAC与DAC为面的二面角θ的大小.
(3)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
(Ⅰ)证明FO∥平面CDE;
(Ⅱ)设BC=3CD,证明EO⊥平面CDF.
查看答案和解析>>
科目: 来源: 题型:
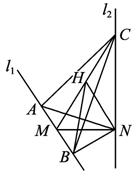
(Ⅰ)证明AC⊥NB;
(Ⅱ)若∠ACB=60°,求NB与平面ABC所成角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
(1)证明面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求面AMC与面BMC所成二面角的大小.
查看答案和解析>>
科目: 来源: 题型:
A.1 B.2 C.3 D.4
查看答案和解析>>
科目: 来源: 题型:
(1)求双曲线C2的方程;
(2)若直线l:y=kx+![]() 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足![]() ·
·![]() <6(其中O为原点),求k的取值范围.
<6(其中O为原点),求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com