练习册

  • 练习册
  • 试题
    相关习题
     0  57712  57720  57726  57730  57736  57738  57742  57748  57750  57756  57762  57766  57768  57772  57778  57780  57786  57790  57792  57796  57798  57802  57804  57806  57807  57808  57810  57811  57812  57814  57816  57820  57822  57826  57828  57832  57838  57840  57846  57850  57852  57856  57862  57868  57870  57876  57880  57882  57888  57892  57898  57906  266669 

    科目： 来源： 题型：

    函数y=cos(4x+)的图象的两条相邻对称轴间的距离为

    A.               B.                C.                D.π

    查看答案和解析>>

    科目： 来源： 题型：

    设集合A={x|1≤x≤2},B={x|x≥a}.若AB,则a的范围是

    A.a＜1              B.a≤1              C.a＜2               D.a≤2

    查看答案和解析>>

    科目： 来源： 题型：

    已知数列{an}的前n项和为Sn,a1=,且2Sn=2Sn-1+2an-1+1(n≥2,n∈N*).数列{bn}满足b1=,且3bn-bn-1=n(n≥2,n∈N*).

    (1)求证:数列{an}为等差数列;

    (2)求证:数列{bn-an}为等比数列;

    (3)求数列{bn}的通项公式以及前n项和Tn.

    查看答案和解析>>

    科目： 来源： 题型：

    已知抛物线x2=2py(p＞0),过焦点F的动直线l交抛物线于A、B两点,抛物线在A、B两点处的切线相交于点Q,O为坐标原点.

    (1)求·的值;

    (2)求点Q的纵坐标;

    (3)证明||2=||·||.

    查看答案和解析>>

    科目： 来源： 题型：

    有甲、乙、丙、丁四名网球运动员,通过对过去战绩的统计,在一场比赛中,甲对乙、丙、丁取胜的概率分别为0.6、0.8、0.9.

    (1)若甲和乙之间进行三场比赛,求甲恰好胜两场的概率;

    (2)若四名运动员每两人之间进行一场比赛,求甲恰好胜两场的概率;

    (3)若四名运动员每两人之间进行一场比赛,设甲获胜场次为ξ,求随机变量ξ的分布列及期望Eξ.

    查看答案和解析>>

    科目： 来源： 题型：

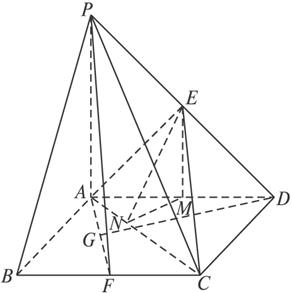
    如图,四棱锥P—ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.

    (1)求证:PA⊥平面ABCD;

    (2)求二面角E-AC-D的大小;

    (3)在线段BC上是否存在点F,使得点E到平面PAF的距离为?若存在,确定点F的位置;若不存在,请说明理由.

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f(x)=x3+ax2+bx(a,b∈R)的图象过点P(1,f(1)),且在点P处的切线的方程为y=8x-6.

    (1)求a,b的值;

    (2)求函数f(x)的单调区间;

    (3)求函数f(sinx)的最值.

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f(x)=coscos-sinsin+2sinxcosx.

    (1)求f()的值;

    (2)求f(x)的最大值并指出相应的x的取值集合.

    查看答案和解析>>

    科目： 来源： 题型：

    已知符号函数sgnx=则不等式(x+1)sgnx＞2的解集是______________.

    查看答案和解析>>

    科目： 来源： 题型：

    已知△ABC中,AB=AC,则cosB+cosA的最大值为______________.

    查看答案和解析>>

    同步练习册答案