如果存在正项数列{a_n}满足:a₁=,f(a₁)+f(a₂)+f(a₃)+…+f(a_n)-n=a₁³+a₂³+a₃³+…+a_n³-n²a_n(n∈N^*).

(1)求数列{a_n}的通项;

(2)求证:+++…+＜1;

(3)求证:+++…+＜1+.

(1)若x≥0,求动点P(x,)轨迹C的方程;

(2)若a=2,不过原点的直线l与x轴,y轴的交点分别为T,S,并且与(1)中轨迹C交于不同的两点P,Q,试求+的取值范围;

(3)设P(x,y)是平面上的任一点,定义d₁(P)=,d₂(P)=.若在(1)中轨迹C上存在不同的两点A₁,A₂,使得d₁(A_i)=d₂(A_i)(i=1,2)成立,求实数a的取值范围.

(1)求函数y=f(x)的表达式;

(2)若x＞0,证明:f(x)＞;

(3)若x∈［-1,1］时,不等式x²≤f(x²)+m²m-3都恒成立,求实数m的取值范围.

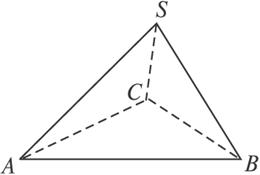
(1)求证:AC⊥SB;

(2)求二面角S-BC-A的正切值.

(1)求在前三次摸球中,甲摸得红球的次数ξ的数学期望;

(2)设第n次由甲摸球的概率为a_n,试建立a_n+1与a_n的递推关系.

(1)设x=x₀是函数y=f(x)图象的一条对称轴,求g(x₀)的值;

(2)求使函数h(x)=f()+g()(ω＞0)在区间［,］上是增函数的ω的最大值.

①若f(x)=2x³+mx²+3的反函数为f^-1(x),则f^-1(5)=1;

②过原点作圆x²+y²-12x+9=0的两切线,则两切线所夹的劣弧长为2π;

③若α、β是第一象限角,则“α＞βtanα＞tanβ”的逆命题是真命题;

④在样本频率分布直方图中,共有三个长方形,其面积由小到大构成等差数列{a_n},且a₂+a₃=0.8,则最大的小长方形的面积为.

其中正确命题的序号为____________.

若两正数a,b满足f(2a+b)＜1,则的取值范围是____________.