
科目: 来源: 题型:
(1)试求m的值,并分别写出x′和y′用x、y表示的关系式;
(2)将(x,y)作为点P的坐标,(x′,y′)作为点Q的坐标,上述关系式可以看作是坐标平面上点的一个变换:它将平面上的点P变到这一平面上的点Q.
当点P在直线y=x+1上移动时,试求点P经该变换后得到的点Q的轨迹方程.
(3)是否存在这样的直线:它上面的任一点经上述变换后得到的点仍在c 该直线上?若存在,试求出所有这些直线;若不存在,则说明理由.
查看答案和解析>>
科目: 来源: 题型:
(1)求点Pn的纵坐标bn的表达式;
(2)若对每个自然数n,以bn,bn-1,bn-2为边长能构成一个三角形,求a的取值范围;
(3)设Bn=b1b2…bn(n![]() N).若a取(2)中确定的范围内的最小整数,求数列
N).若a取(2)中确定的范围内的最小整数,求数列![]() 的最大项的项数.
的最大项的项数.
查看答案和解析>>
科目: 来源: 题型:

(1)现机器人在直角坐标系的坐标原点,且面对x轴正方向.试给机器人下一个指令,使其移动到
点(4,4).
(2)机器人在完成该指令后,发现在点(17,0)外有一小球正向坐标原点作匀速直线滚动.已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令(结果精确到小数点后两位).
查看答案和解析>>
科目: 来源: 题型:
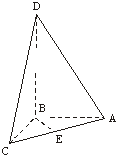
18.如图所示四面体ABCD中,AB、BC、BD两两互相垂直,且AB=BC=2,E是AC中点,异面直线
AD与BE所成的角的大小为arccos![]() .求四面体ABCD的体积.
.求四面体ABCD的体积.
查看答案和解析>>
科目: 来源: 题型:
A.若点P(a,2a)(a≠0)为角![]() 终边上一点,则sin
终边上一点,则sin![]() =
=![]() .
.
B.同时满足sin![]() =
=![]() cos
cos![]() =
=![]() 的角
的角![]() 有且只有一个.
有且只有一个.
C.当![]() <1时,tan(arcsin
<1时,tan(arcsin![]() )的值恒正.
)的值恒正.
D.三角方程tan(x+![]() )=
)=![]() 的解集为{x
的解集为{x![]() x=k
x=k![]() ,k
,k![]() Z}.
Z}.
查看答案和解析>>
科目: 来源: 题型:
(1)若a∥![]() ,b∥
,b∥![]() ,则a∥b.
,则a∥b.
(2)若a∥![]() ,a∥
,a∥![]() ,则
,则![]() ∥
∥![]() .
.
(3)若![]()
![]()
![]() ,
,![]() ,则
,则![]() ∥
∥![]() .
.
其中正确的个数是………………………………………………( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com