
科目: 来源: 题型:
在一个袋子中放9个白球,1个红球,摇匀后随机摸球:
每次摸出球后记下球的颜色然后放回袋中;
每次摸出球后不放回袋中.
在两种情况下分别做10次试验,求每种情况下第4次摸到红球的频率.两个频率相差得远吗?两个事件的概率一样吗?第4次摸到红球的频率与第1次摸到红球的频率相差得远吗?请说明原因.
查看答案和解析>>
科目: 来源: 题型:
圆锥的轴截面SAB是边长为2的等边三角形,O为底面中心,M为SO的中点,动点P在圆锥底面内(包括圆周)。若AM⊥MP,则P点形成的轨迹的长度为( )
A. ![]() B.
B. ![]() C. 3 D.
C. 3 D.![]()
查看答案和解析>>
科目: 来源: 题型:
已知抛物线C的一个焦点为F(![]() ,0),对应于这个焦点的准线方程为x=-
,0),对应于这个焦点的准线方程为x=-![]() .
.
(1)写出抛物线C的方程;
(2)过F点的直线与曲线C交于A、B两点,O点为坐标原点,求△AOB重心G的轨迹方程;
(3)点P是抛物线C上的动点,过点P作圆(x-3)2+y2=2的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?求出|MN|的最小值.
查看答案和解析>>
科目: 来源: 题型:
为抗击金融风暴,某工贸系统决定对所属企业给予低息贷款的扶持.该系统先根据相关评分标准对各个企业进行了评估,并依据评估得分将这些企业分别评定为优秀、良好、合格、不合格4个等级,然后根据评估等级分配相应的低息贷款金额,其评估标准和贷款金额如下表:
| 评估得分 | [50,60) | [60,70) | [70,80) | [80,90] |
| 评定类型 | 不合格 | 合格 | 良好 | 优秀 |
| 贷款金额(万元) | 0 | 200 | 400 | 800 |
为了更好地掌控贷款总额,该系统随机抽查了所属部分企业的评估分数,得其频率分布直方图如下:
(Ⅰ)估计该系统所属企业评估得分的中位数;
(Ⅱ)该系统要求各企业对照评分标准进行整改,若整改后优秀企业数量不变,不合格企业、合格企业、良好企业的数量依次成等差数列,系统所属企业获得贷款的均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数的百分比的最大值是多少?

查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分) 如图,圆柱的轴截面AB![]() CD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π.
CD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π.
(Ⅰ)求证:AF⊥BD;
(Ⅱ)求直线DE与平面ABCD所成角的正切值.
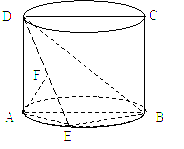
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com