
科目: 来源: 题型:
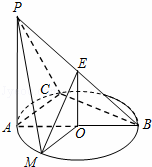
如图所示,AB是⊙O的直径,点C是⊙O圆周上不同于A、B的任意一点,PA⊥平面ABC,点E是线段PB的中点,点M在![]() 上,且MO∥AC.
上,且MO∥AC.
(1)求证:BC⊥平面PAC;
(2)求证:平面EOM∥平面PAC.
查看答案和解析>>
科目: 来源: 题型:
对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
| [3,6) | 10 | m |
| [6,9) | n | p |
| [9,12) | 4 | q |
| [12,15] | 2 | 0.05 |
| 合计 | N | 1 |
(1)求出表中N,p及图中a的值;
(2)在所取样本中,从参加社区服务的次数不少于9次的学生中任选2人,求至少有一人参加社区服务次数在区间[12,15]内的概率.

查看答案和解析>>
科目: 来源: 题型:
在平面直角坐标系xOy中,已知A(3,1),C(1,0).
(1)求以点C为圆心,且经过点A的圆C的标准方程;
(2)若直线l的方程为x﹣2y+9=0,判断直线l与(1)中圆C的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
设函数f(x)的定义域为R,若存在与x无关的正常数M,使|f(x)|≤M|x|对一切实数x恒成立,则称f(x)为有界泛函.有下面四个函数:
①f(x)=1;
②f(x)=x2;
③f(x)=2xsinx;
④![]() .
.
其中属于有界泛函的是( )
|
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目: 来源: 题型:
已知等差数列{an}的首项为4,公差为4,其前n项和为Sn,则数列 {![]() }的前n项和为( )
}的前n项和为( )
|
| A. |
| B. |
| C. |
| D. |
|
| 考点: | 数列的求和;等差数列的性质. |
| 专题: | 等差数列与等比数列. |
| 分析: | 利用等差数列的前n项和即可得出Sn,再利用“裂项求和”即可得出数列 { |
| 解答: | 解:∵Sn=4n+ ∴ ∴数列 { 故选A. |
| 点评: | 熟练掌握等差数列的前n项和公式、“裂项求和”是解题的关键. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com