
科目: 来源:2014届湖南师大附中高三第二次月考理科数学试卷(解析版) 题型:填空题
某种机器的使用年限 和所支出的维修费用
和所支出的维修费用 (万元)有下表的统计资料:
(万元)有下表的统计资料:
|
|
2 |
3 |
4 |
5 |
6 |
|
|
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
根据上表可得回归方程 ,据此模型估计,该种机器使用年限为10年时
,据此模型估计,该种机器使用年限为10年时
维修费用约 万元(结果保留两位小数).
查看答案和解析>>
科目: 来源:2014届湖南师大附中高三第二次月考理科数学试卷(解析版) 题型:填空题
对于函数f(x),若在其定义域内存在两个实数a,b(a<b),使当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“布林函数”,区间[a,b]称为函数f(x)的“等域区间”.
(1)布林函数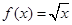 的等域区间是 .
的等域区间是 .
(2)若函数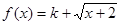 是布林函数,则实数k的取值范围是
.
是布林函数,则实数k的取值范围是
.
查看答案和解析>>
科目: 来源:2014届湖南师大附中高三第二次月考理科数学试卷(解析版) 题型:解答题
已知向量 ,设函数
,设函数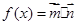
(1)求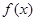 在区间
在区间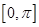 上的零点;
上的零点;
(2)在 中,角
中,角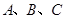 的对边分别是
的对边分别是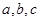 ,且满足
,且满足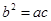 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2014届湖南师大附中高三第二次月考理科数学试卷(解析版) 题型:解答题
一个袋子里装有7个球,其中有红球4个, 编号分别为1,2,3,4;白球3个,编号分别为1,2,3.从袋子中任取4个球(假设取到任何一个球的可能性相同).
(Ⅰ)求取出的4个球中, 含有编号为3的球的概率;
(Ⅱ)在取出的4个球中, 红球编号的最大值设为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目: 来源:2014届湖南师大附中高三第二次月考理科数学试卷(解析版) 题型:解答题
知椭圆 的离心率为
的离心率为 ,定点
,定点 ,椭圆短轴的端点是
,椭圆短轴的端点是 ,且
,且 .
.
(1)求椭圆 的方程;
的方程;
(2)设过点 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆 于
于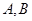 两点.试问
两点.试问 轴上是否存在异于
轴上是否存在异于 的定点
的定点 ,使
,使 平分
平分 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2014届湖南师大附中高三第二次月考理科数学试卷(解析版) 题型:解答题
某企业为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的设备维修、燃料和动力等消耗的费用(称为设备的低劣化值)会逐年增加,第一年设备低劣化值是4万元,从第二年到第七年,每年设备低劣化值均比上年增加2万元,从第八年开始,每年设备低劣化值比上年增加25%.
(1)设第 年该生产线设备低劣化值为
年该生产线设备低劣化值为 ,求
,求 的表达式;
的表达式;
(2)若该生产线前 年设备低劣化平均值为
年设备低劣化平均值为 ,当
,当 达到或超过12万元时,则当年需要更新生产线,试判断第几年需要更新该生产线,并说明理由.
达到或超过12万元时,则当年需要更新生产线,试判断第几年需要更新该生产线,并说明理由.
查看答案和解析>>
科目: 来源:2014届湖南师大附中高三第二次月考理科数学试卷(解析版) 题型:解答题
已知函数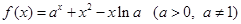 .
.
(1)求函数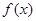 的单调区间;
的单调区间;
(2)若函数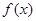 满足:
满足:
①对任意的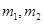 ,
,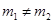 ,当
,当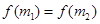 时,有
时,有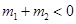 成立;
成立;
②对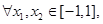
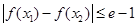 恒成立.求实数
恒成立.求实数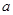 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com