
【题目】如图①,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,四边形
,四边形![]() 是边长为
是边长为![]() 的正方形,点
的正方形,点![]() 分别在边
分别在边![]() 上,此时
上,此时![]() ,
,![]() 成立.
成立.
(1)当正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②,
,如图②,![]() 成立吗?若成立,请证明;若不成立,请说明理由;
成立吗?若成立,请证明;若不成立,请说明理由;
(2)当正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (任意角)时,
(任意角)时,![]() 仍成立吗?直接回答;
仍成立吗?直接回答;
(3)连接![]() ,当正方形
,当正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 时,是否存在
时,是否存在![]() ∥
∥![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
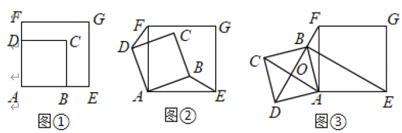
【答案】(1)成立,证明见解析;(2)结论仍成立;(3)存在,![]()
【解析】
(1)先利用正方形的性质和旋转的性质证明![]() ≌
≌![]() ,然后得出
,然后得出![]() ,再根据等量代换即可得出
,再根据等量代换即可得出![]() ,则有
,则有![]() ;
;
(2)先利用正方形的性质和旋转的性质证明![]() ≌
≌![]() ,然后得出
,然后得出![]() ,再根据等量代换即可得出
,再根据等量代换即可得出![]() ,则有
,则有![]() ;
;
(3)通过分析得出![]() 时,
时,![]() 在同一直线上,根据AO,AF求
在同一直线上,根据AO,AF求![]() ,从而有
,从而有![]() ,最后利用
,最后利用![]() 即可求解.
即可求解.
(1)结论![]() ,
,![]() 仍成立.
仍成立.
如图1,延长![]() 交
交![]() 于
于![]() 交
交![]() 于点
于点![]() ,
,

∵四边形![]() ,ABCD都是正方形,
,ABCD都是正方形,
∴![]() .
.
由旋转可得,![]() ,
,
![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
![]()
![]() ,
,
![]() ,
,
∴![]() ,
,
∴结论仍成立 .
(2)若正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 时,如图,结论仍然成立,理由如下:
时,如图,结论仍然成立,理由如下:

如图2,延长![]() 交
交![]() 于
于![]() 交
交![]() 于点
于点![]() ,
,
∵四边形![]() ,ABCD都是正方形,
,ABCD都是正方形,
∴![]() .
.
由旋转可得,![]() ,
,
![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
![]()
![]() ,
,
![]() ,
,
∴![]() ,
,
∴结论仍成立 .
当旋转其他角度时同理可证![]() ,所以结论仍成立.
,所以结论仍成立.
(3)存在
如图3,连接![]() ,与
,与![]() 相交于
相交于![]() ,
,

∵![]() ,当
,当![]() ∥
∥![]() 时,
时,![]() ,
,
又∵![]() ,
,
∴![]() 在同一直线上.
在同一直线上.
∵四边形ABCD,AEGF是正方形,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]()
即当![]() 时,
时,![]() ∥
∥![]() 成立.
成立.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点D坐标为(2,﹣1),且过点B(3,0),与y轴交于点C.
(1)求抛物线的解析式及点C的坐标;
(2)连结OD、CD、CB,CD交x轴于点E,求S△CEB:S△ODE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的m个小球,其中 5 个黑球, 从袋中随机摸出一球,记下其颜色,这称为依次摸球试验,之后把它放回袋 中,搅匀后,再继续摸出一球.以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
摸出黑球次数 | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
根据列表,可以估计出 m 的值是( )
A. 5 B. 10 C. 15 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() 为
为![]() 边上一点.
边上一点.
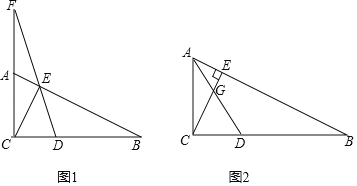
(1)当![]() 时,直接写出
时,直接写出![]() ,
,![]() .
.
(2)如图1,当![]() ,
,![]() 时,连
时,连![]() 并延长交
并延长交![]() 延长线于
延长线于![]() ,求证:
,求证:![]() .
.
(3)如图2,连![]() 交
交![]() 于
于![]() ,当
,当![]() 且
且![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列10×10的网格中,横、纵坐标均为整数的点叫做格点,例如A(3,0),B(4,3)都是格点.将△AOB绕点O顺时针旋转90°得到△COD(点A,B的对应点分别为点C,D).
(1)作出△COD;
(2)下面仅用无刻度的直尺画△AOD的内心I,操作如下:
第一步:在x轴上找一格点E,连接DE,使OE=OD;
第二步:在DE上找一点F,连接OF,使OF平分∠AOD;
第三步:找格点G,得到正方形OAGC,连接AC,则AC与OF的交点I是△OAD的内心.
请你按步骤完成作图,并直接写出E,F,I三点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
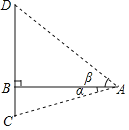
A.asinα+asinβB.acosα+acosβC.atanα+atanβD.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com