
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点D坐标为(2,﹣1),且过点B(3,0),与y轴交于点C.
(1)求抛物线的解析式及点C的坐标;
(2)连结OD、CD、CB,CD交x轴于点E,求S△CEB:S△ODE.

【答案】(1)y=x2﹣4x+3,点C(0,3);(2)3:1.
【解析】
(1)抛物线的表达式为:y=a(x﹣2)2﹣1,将点B的坐标代入上式并解得:a=1,即可求解;
(2)直线CD的表达式为:y=﹣2x+3,则点E(![]() ,0),S△CEB=
,0),S△CEB=![]() ×EB×OC=
×EB×OC=![]() ,S△ODE=
,S△ODE=![]() ×OE×|yD|=
×OE×|yD|=![]() ,即可求解.
,即可求解.
解:(1)抛物线的表达式为:y=a(x﹣2)2﹣1,
将点B的坐标代入上式并解得:a=1,
故抛物线的表达式为:y=x2﹣4x+3,
则点C(0,3);
(2)将点C、D的坐标代入一次函数表达式:y=mx+n并解得:
直线CD的表达式为:y=﹣2x+3,
则点E(![]() ,0),
,0),
S△CEB=![]() ×EB×OC=
×EB×OC=![]() ,
,
S△ODE=![]() ×OE×|yD|=
×OE×|yD|=![]() ,
,
故S△CEB:S△ODE=3:1.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
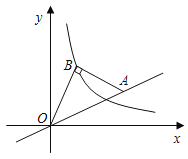
【题目】如图,直线y=ax经过点A(4,2),点B在双曲线y=![]() (x>0)的图象上,连结OB、AB,若∠ABO=90°,BA=BO,则k的值为_____.
(x>0)的图象上,连结OB、AB,若∠ABO=90°,BA=BO,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
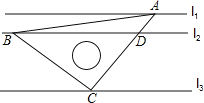
【题目】如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图所示放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A(4,0),B两点,与y轴交于点C(0,2),对称轴x=1,与x轴交于点H.

(1)求抛物线的函数表达式;
(2)直线y=kx+1(k≠0)与y轴交于点E,与抛物线交于点 P,Q(点P在y轴左侧,点Q在y轴右侧),连接CP,CQ,若△CPQ的面积为![]() ,求点P,Q的坐标;
,求点P,Q的坐标;
(3)在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G顺时针旋转90°,使点K恰好落在抛物线上,若存在,请直接写出点K的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 分别交
分别交![]() 、
、![]() 轴于
轴于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一交点为
轴的另一交点为![]() .
.
(1)求![]() 、
、![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度向点
出发,以每秒1个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
①当![]() 为何值时,线段
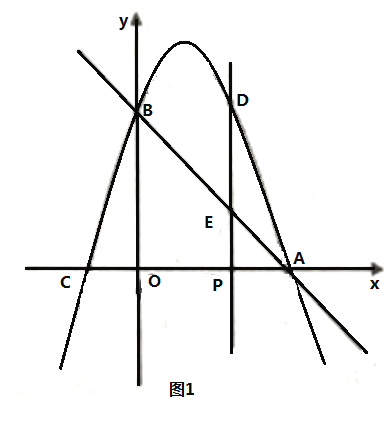
为何值时,线段![]() 长度最大,最大值是多少?(如图1)
长度最大,最大值是多少?(如图1)
②过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,若
,若![]() 与
与![]() 相似,求
相似,求![]() 的值(如图2)
的值(如图2)

查看答案和解析>>
科目:初中数学 来源: 题型:
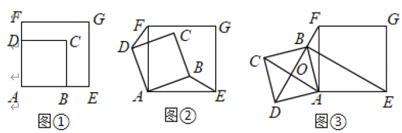
【题目】如图①,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,四边形
,四边形![]() 是边长为
是边长为![]() 的正方形,点
的正方形,点![]() 分别在边
分别在边![]() 上,此时
上,此时![]() ,
,![]() 成立.
成立.
(1)当正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②,
,如图②,![]() 成立吗?若成立,请证明;若不成立,请说明理由;
成立吗?若成立,请证明;若不成立,请说明理由;
(2)当正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (任意角)时,
(任意角)时,![]() 仍成立吗?直接回答;
仍成立吗?直接回答;
(3)连接![]() ,当正方形
,当正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 时,是否存在
时,是否存在![]() ∥
∥![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com