
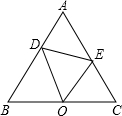
 如图,△ABC是等边三角形,点O是BC上一点,点E在AC上,点D在AB上,若OD平分∠BDE,OE平分∠CED.求证:BO=CO.
如图,△ABC是等边三角形,点O是BC上一点,点E在AC上,点D在AB上,若OD平分∠BDE,OE平分∠CED.求证:BO=CO.  星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
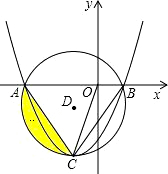 已知:如图,抛物线y=ax2+bx+c的顶点C在以D(-3,-3)为圆心,6为半径的圆上,且经过⊙D与x轴的两个交点A、B,连结AC、BC、OC.
已知:如图,抛物线y=ax2+bx+c的顶点C在以D(-3,-3)为圆心,6为半径的圆上,且经过⊙D与x轴的两个交点A、B,连结AC、BC、OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 顶点数 | 面数 | 棱数 | 顶点数+面数-棱数 | |
| 四棱锥 | 5 | 5 | 8 | 2 |
| 五棱锥 | 6 | 6 | 10 | 2 |
| 六棱锥 | 7 | 7 | 12 | 2 |
| 八棱锥 | 9 | 9 | 16 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明的妈妈让他在无法看到袋子里糖果的情形下从袋子里抽出一颗糖果.袋子里有三种颜色的糖果,它们的大小、形状、质量等都相同,其中所有糖果的数量统计如图所示.小明抽到红色糖果的概率为( )
小明的妈妈让他在无法看到袋子里糖果的情形下从袋子里抽出一颗糖果.袋子里有三种颜色的糖果,它们的大小、形状、质量等都相同,其中所有糖果的数量统计如图所示.小明抽到红色糖果的概率为( )| A. | $\frac{5}{18}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{15}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com