
【题目】定义:如果一元二次方程![]() 满足
满足![]() ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知![]() 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图①,在矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 运动,速度为每秒2个单位长度;点
运动,速度为每秒2个单位长度;点![]() 从点
从点![]() 出发向点
出发向点![]() 运动,速度为每秒1个单位长度.
运动,速度为每秒1个单位长度.![]() 、
、![]() 两点同时出发,点
两点同时出发,点![]() 运动到点
运动到点![]() 时,两点同时停止运动,设点
时,两点同时停止运动,设点![]() 的运动时间为
的运动时间为![]() (秒).连结
(秒).连结![]() 、
、![]() 、
、![]() 、
、![]() .
.
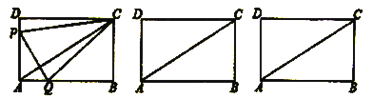
(1)点![]() 到点
到点![]() 时,
时,![]() ____________;当点
____________;当点![]() 到终点时,
到终点时,![]() 的长度为_________;
的长度为_________;
(2)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)当![]() 的面积为9时,求
的面积为9时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE =∠C
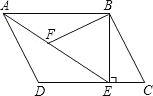
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30°,求AE的长;
(3)在(1)、(2)的条件下,若AD=3,求BF的长(计算结果可含根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已 知直线![]() 交坐标轴于
交坐标轴于![]() 两点,以线段
两点,以线段![]() 为边向上作正方形
为边向上作正方形![]() ,过点
,过点![]() 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为![]() .
.
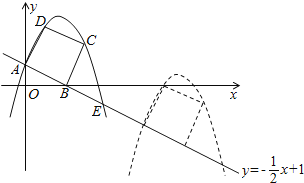
(1)请直接写出点![]() 的坐标;
的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 下滑,直至顶点
下滑,直至顶点![]() 落在x轴上时停止.设正方形落在
落在x轴上时停止.设正方形落在![]() 轴下方部分的面积为
轴下方部分的面积为![]() ,求
,求![]() 关于滑行时间
关于滑行时间![]() 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量![]() 的取值范围;
的取值范围;
(4)在(3)的条件下,抛物线与正方形一起平移,同时停止,求抛物线上![]() 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0
(1)证明原方程有两个不相等的实数根;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示:AB=|x1﹣x2|)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点 C的对应点 C′恰好落在CB的延长线上,边AB交边 C′D′于点E.
(1)求证:BC=BC′;
(2)若 AB=2,BC=1,求AE的长.
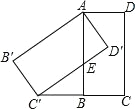
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com