Question

如图①E、F、G、H为正方形ABCD各边延长线上的点，CE=BC，DF=CD，AG=DA，BH=AB，若正方形ABCD的面积等于1．
（1）请你求出四边形EFGH的面积；
（2）如图②，图③，若将正方形ABCD变为矩形和菱形，其他条件仍然不变，请你分别写出四边形EFGH的面积．
（3）如图④，若将正方形ABCD变为任意四边形，其他条件仍然不变，请你猜想四边形EFGH的面积并说明理由．

Answer 1

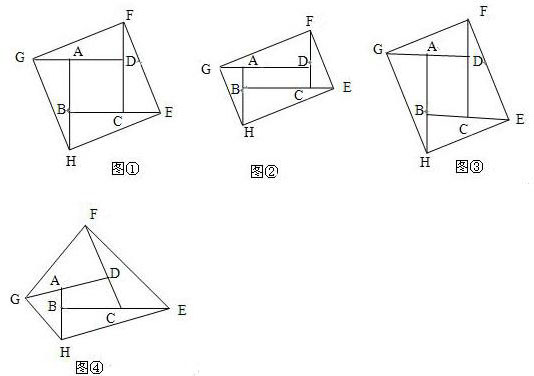
解：（1）∵四边形ABCD的面积等于1，
∴BH=BC=1，
∴BE=2，
∴S_△BEH=1，
同理S_△AGH=S_△DGF=S_△FCE=S_△BEH=1，
∴四边形EFGH的面积为5；

（2）∵矩形ABCD的面积为1，
∴CD•BC=1，
∵CE=BC，DF=CD，
∴S_△ECF=CE•CF=CD•2BC=1，
同理S_△AGH=S_△DGF=S_△FCE=S_△BEH=1，
∴四边形EFGH的面积均为5；

（3）依题意可知CE=BC，DF=CD，AG=DA，BH=AB，
故S_△AGH=S_△DGF=S_△FCE=S_△BEH=1
所以四边形面积仍为5．
分析：（1）依题意已知四边形ABCD的面积为1，可推出BH=BC=1，求得BE=2，S_△BEH=1，故同理证得S_△AGH=S_△DGF=S_△FCE=S_△BEH=1，故四边形面积为四个三角形以及一个四边形的和为5；
（2）依题意可知矩形ABCD的面积为1，其余四个三角形可证明其两两全等，然后根据（1）的证明方法可证得四边形EFGH的面积为5；
（3）依题意可知CE=BC，DF=CD，AG=DA，BH=AB，可证得四个三角形的面积相等，从而得出四边形的面积．
点评：本题考查的是正方形的性质，考生注意总结规律解答题目．