
 小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?
小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远? 分析 设出平路和坡路的路程,从家里到学校走平路和下坡路一共用10分钟,从学校到家里走上坡路和平路一共用15分钟,利用这两个关系式列出方程组解答即可.
解答 解:设平路有xm,下坡路有ym,
根据题意得$\left\{\begin{array}{l}{\frac{x}{60}+\frac{y}{80}=10}\\{\frac{x}{60}+\frac{y}{40}=15}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=300}\\{y=400}\end{array}\right.$,
答:小华家到学校的平路和下坡路各为300m,400m.
点评 本题考查了二元一次方程的应用,此题主要利用时间、速度、路程三者之间的关系解答,注意来回坡路的变化是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )| A. | 相离 | B. | 相交 | ||
| C. | 相切 | D. | 以上三种情况均有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,-2) | B. | (-2,-3) | C. | (1,-6) | D. | (-6,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
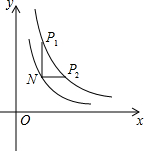 如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )
如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )| A. | $\frac{1}{2}$或2 | B. | $\frac{1}{2}$或8 | C. | 2或6 | D. | 2或8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com