
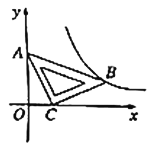
【题目】在平面直角坐标系![]() 中,将一块含有
中,将一块含有![]() 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿![]() 轴正方向平移,当顶点
轴正方向平移,当顶点![]() 恰好落在该双曲线上时停止运动,则此时点
恰好落在该双曲线上时停止运动,则此时点![]() 的对应点
的对应点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
过B点作BD⊥x轴,根据等腰直角三角形的性质证明△OAC≌△DCB,即可求出B点坐标,即可求出反比例函数解析式,再求出顶点![]() 运动到双曲线平移的距离,即可求出C’的坐标.
运动到双曲线平移的距离,即可求出C’的坐标.
过B点作BD⊥x轴,
∵∠ACO+∠BCD=90°,∠OAC+∠ACO=90°,
∴∠BCD=∠OAC,又AC=CB,∠AOC=∠CDB=90°,
∴△OAC≌△DCB
∴OC=BD,OA=CD,
∵A(0,2),C(1,0)
∴OD=3,BD=1
∴B(3,1)
设反比例函数为y=![]() ,把(3,1)代入求解k=3,
,把(3,1)代入求解k=3,
∴y=![]() ,
,
把y=2代入![]() ,解得x=
,解得x=![]()
∵顶点![]() 恰好落在该双曲线上时停止运动,
恰好落在该双曲线上时停止运动,
故A点向右平移了![]() 个单位,
个单位,
所以此时点![]() 的对应点
的对应点![]() 的坐标为
的坐标为![]()
故选B.



 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】某电台“市民热线”对上周内接到的热线电话进行了分类统计,得到的统计信息图如图所示,其中有关房产城建的电话有30个,请你根据统计图的信息回答以下问题:
(1)道路交通热线电话是多少个占总数百分比是多少?
(2)上周“市民热线”接到有关环境保护方面的电话有多少个?
(3)据此估计,除环境保护方面的电话外,“市民热线”今年(按52周计算)将接到的热线电话约多少个?
(4)为了更直观显示各类“市民热线”电话的数目,你准备采用什么样的统计方法?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,16,4分)如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .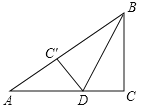
查看答案和解析>>
科目:初中数学 来源: 题型:
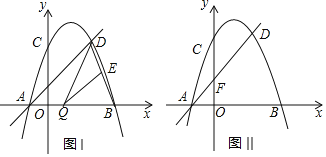
【题目】抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B,C的坐标分别为(4,0)和(0,4),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).
(1)求抛物线和直线AD的解析式;
(2)如图Ⅰ,点Q是线段AB上一动点,过点Q作QE∥AD,交BD于点E,连接DQ,求△QED面积的最大值;
(3)如图Ⅱ,直线AD交y轴于点F,点M,N分别是抛物线对称轴和抛物线上的点,若以C,F,M,N为顶点的四边形是平行四边形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | 200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
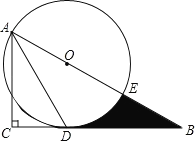
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某单位要建一个面积为48 m2的小仓库,小仓库有一边靠墙(墙长10m),并在与墙平行的一边开一道宽1 m的门,现有能围成19 m的木板,求小仓库的长与宽?
(注意:仓库靠墙的那一边不能超过墙长).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将小球沿地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度y(m)与它的飞行时间x(s)满足二次函数关系,y与x的几组对应值如表所示:


(1)求y关于x的函数解析式(不要求写x的取值范围);
(2)问:小球的飞行高度能否达到20.5m?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 经过点
经过点![]() ,
,![]() 、
、![]() ,
,![]() ,其中
,其中![]() 、
、![]() 是方程
是方程![]() 的两根,且
的两根,且![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线只有一个公共点
与抛物线只有一个公共点
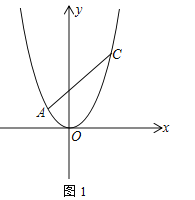
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)求直线![]() 的解析式;
的解析式;
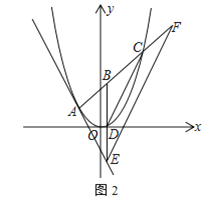
(3)如图2,点![]() 是线段
是线段![]() 上的动点,若过点
上的动点,若过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与抛物线相交于点
,与抛物线相交于点![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com