
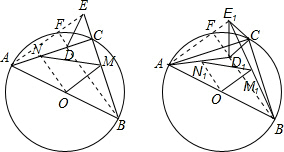
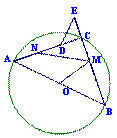
 如图甲,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角△DCE中,∠DCE是直角,点D在线段AC上.
如图甲,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角△DCE中,∠DCE是直角,点D在线段AC上.| MN |
| OM |
| MN |
| OM |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| MN |
| ON |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
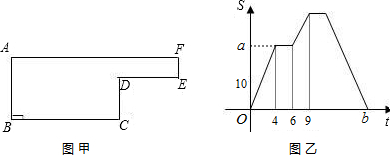 移动,相应的△ABP的面积S关于时间t的函数图象如图所示,若AB=6cm,试回答下列问题:
移动,相应的△ABP的面积S关于时间t的函数图象如图所示,若AB=6cm,试回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
如图甲,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角△DCE中,∠DCE是直角,点D在线段AC上.
(1)问B、C、E三点在一条直线上吗?为什么?
(2)若M是线段BE的中点,N是线段AD的中点,试求![]() 的值;
的值;
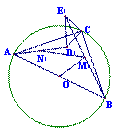
(3)将△DCE绕点C逆时针旋转α(O°<α<90°)后,记为△D![]() CE
CE![]() (图乙),若M
(图乙),若M![]() 是线段BE
是线段BE![]() 的中点,N
的中点,N![]() 是线段AD
是线段AD![]() 的中点,则
的中点,则![]() =____
=____
查看答案和解析>>
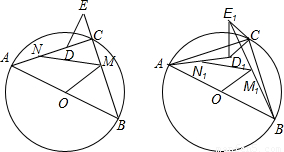
科目:初中数学 来源:2011-2012学年湖北省武汉市青山区九年级(上)期中数学试卷(解析版) 题型:解答题
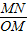 的值;
的值; =______
=______
查看答案和解析>>
科目:初中数学 来源:福建省中考真题 题型:解答题
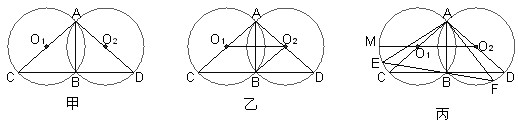
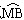 上任取一点E(点E与点B不重合),EB的延长线交优弧
上任取一点E(点E与点B不重合),EB的延长线交优弧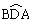 于点F,如图丙所示,连接AE、AF,则AE______AB(请在横线上填上“≥、≤、<、>”这四个不等号中的一个)并加以证明。
于点F,如图丙所示,连接AE、AF,则AE______AB(请在横线上填上“≥、≤、<、>”这四个不等号中的一个)并加以证明。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com