
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
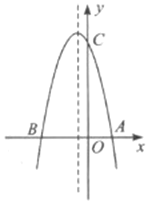
(1)求该抛物线的解析式;
(2)若抛物线交![]() 轴于
轴于![]() 点,在该抛物线的对称轴上是否存在点
点,在该抛物线的对称轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出
的周长最小?若存在,求出![]() 点的坐标;若不存在,请说明理由
点的坐标;若不存在,请说明理由
【答案】(1)![]() ;(2)存在,当
;(2)存在,当![]() 的周长最小时,
的周长最小时,![]() 点的坐标为
点的坐标为![]() .
.
【解析】
(1)直接利用待定系数求出二次函数解析式即可;
(2)首先求出直线BC的解析式,再利用轴对称求最短路线的方法得出答案.
(1)![]() 抛物线
抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点
两点
![]() 解得:
解得:![]()
![]() 该抛物线的解析式为
该抛物线的解析式为![]()
(2)该抛物线的对称轴上存在点![]() ,使得
,使得![]() 的周长最小.
的周长最小.
如解图所示,作点![]() 关于抛物线对称轴的对称点
关于抛物线对称轴的对称点![]() ,连接
,连接![]() ,
,
交对称轴于点![]() ,连接
,连接![]() ,
,
![]() 点
点![]() 关于抛物线对称轴的对称点
关于抛物线对称轴的对称点![]() ,且
,且![]() ,交对称轴于点
,交对称轴于点![]()
![]() ,
,
![]() 的周长为
的周长为![]() ,
,
![]() 为抛物线对称轴上一点,
为抛物线对称轴上一点,
![]() 的周长
的周长![]() ,
,
![]() 当点
当点![]() 处在解图位置时,
处在解图位置时,![]() 的周长最小.
的周长最小.
![]() 在
在![]() 中,当
中,当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() ,
,
![]() 点
点![]() 是点
是点![]() 关于抛物线对称轴直线
关于抛物线对称轴直线![]() 的对称点,且
的对称点,且![]() .
.
设过点![]() 两点的直线
两点的直线![]() 的解析式为:
的解析式为:![]() ,
,
![]() 在
在![]() 直线上,
直线上,
![]() ,解得:
,解得:![]() ,
,
![]() 直线的解析式为:
直线的解析式为:![]() ,
,
![]() 抛物线对称轴为直线
抛物线对称轴为直线![]() ,且
,且![]() 直线与抛物线对称轴交于点
直线与抛物线对称轴交于点![]() ,
,
![]() 在
在![]() 中,当
中,当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 在该抛物线的对称轴上存在点
在该抛物线的对称轴上存在点![]() ,使得
,使得![]() 的周长最小,当
的周长最小,当![]() 的周长最小时,
的周长最小时,![]() 点的坐标为
点的坐标为![]()



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在方格纸中(小正方形的边长为1个单位长度),点![]() ,
,![]() ,
,![]() 都在格点上,以
都在格点上,以![]() 为坐标原点建立平面直角坐标系.
为坐标原点建立平面直角坐标系.
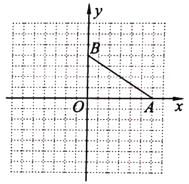
(1)分别写出点![]() ,
,![]() 的坐标:________,画出线段
的坐标:________,画出线段![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 的线段
的线段![]() ;
;
(2)若线段![]() 的中点
的中点![]() 在反比例函数
在反比例函数![]()
![]() 的图象上,则
的图象上,则![]() 的值为________.(直接写出答案)
的值为________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
活动一
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
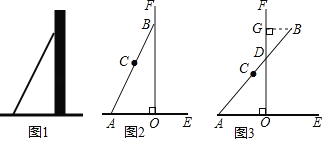
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
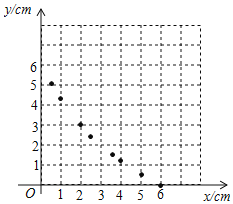
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
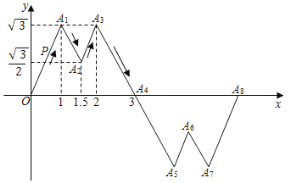
【题目】如图所示,A1(1,![]() ),A2(
),A2(![]() ,
,![]() ),A3(2,
),A3(2,![]() ),A4(3,0).作折线A1A2A3A4关于点A4的中心对称图形,再做出新的折线关于与x轴的下一个交点的中心对称图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线一每秒1个单位的速度移动,设运动时间为t.当t=2020时,点P的坐标为( )
),A4(3,0).作折线A1A2A3A4关于点A4的中心对称图形,再做出新的折线关于与x轴的下一个交点的中心对称图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线一每秒1个单位的速度移动,设运动时间为t.当t=2020时,点P的坐标为( )
A.(1010,![]() )B.(2020,
)B.(2020,![]() )C.(2016,0)D.(1010,
)C.(2016,0)D.(1010,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“五一”国际劳动节,某商场计划购进甲、乙两种品牌的![]() 恤衫共100件,已知乙品牌每件的进价比甲品牌每件的进价贵30元,且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍.
恤衫共100件,已知乙品牌每件的进价比甲品牌每件的进价贵30元,且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍.
(1)求甲、乙两种品牌每件的进价分别是多少元?
(2)商场决定甲品牌以每件50元出售,乙品牌以每件100元出售.为满足市场需求,购进甲种品牌的数量不少于乙种品牌数量的4倍,请你确定获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
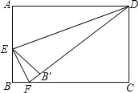
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
A. 2![]() ﹣2B. 6C. 2
﹣2B. 6C. 2![]() ﹣2D. 4
﹣2D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像交
的图像交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,过
,过![]() 画直线。
画直线。
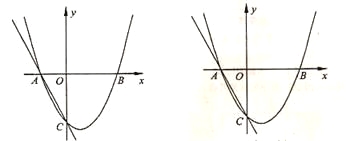
(1)求二次函数的解析式;
(2)点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() ,求
,求![]() 的长;
的长;
(3)点![]() 在二次函数图像上,以
在二次函数图像上,以![]() 为圆心的圆与直线
为圆心的圆与直线![]() 相切,切点为
相切,切点为![]() 。
。
① 点![]() 在
在![]() 轴右侧,且
轴右侧,且![]() (点
(点![]() 与点
与点![]() 对应),求点
对应),求点![]() 的坐标;
的坐标;
② 若![]() 的半径为
的半径为![]() ,求点
,求点![]() 的坐标。
的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2﹣6x+m满足以下条件:当﹣2<x<﹣1时,它的图象位于x轴的下方;当8<x<9时,它的图象位于x轴的上方,则m的值为( )
A.27B.9C.﹣7D.﹣16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com