
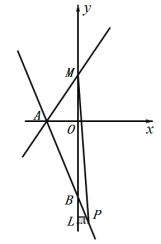
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,直线
,直线![]() 经过点
经过点![]() 和
和![]() .
.

(1)![]() 点的坐标为( , ),
点的坐标为( , ),![]() 点的坐标为( , );
点的坐标为( , );
(2)如图1,已知直线![]() 经过点
经过点![]() 和
和![]() 轴上一点
轴上一点![]() ,
,![]() ,点
,点![]() 在直线AB上且位于
在直线AB上且位于![]() 轴右侧图象上一点,连接
轴右侧图象上一点,连接![]() ,且
,且![]()
![]() .
.
①求![]() 点坐标;
点坐标;
②将![]() 沿直线AM 平移得到
沿直线AM 平移得到![]() ,平移后的点
,平移后的点![]() 与点
与点![]() 重合,
重合,![]() 为
为![]() 上的一动点,当
上的一动点,当![]() 的值最小时,请求出最小值及此时 N 点的坐标;
的值最小时,请求出最小值及此时 N 点的坐标;
(3)如图 2,将点![]() 向左平移 2 个单位到点
向左平移 2 个单位到点![]() ,直线
,直线![]() 经过点
经过点![]() 和
和![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,直线
轴的对称点,直线![]() 经过点
经过点![]() 和点
和点![]() ,动点
,动点![]() 从原点出发沿着
从原点出发沿着![]() 轴正方向运动,连接
轴正方向运动,连接![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,求出
是等腰直角三角形?若存在,求出![]() 点坐标.
点坐标.
【答案】(1)-1,0;0,-3;(2)①点![]() ;②点
;②点![]() ,最小值为
,最小值为![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据两个非负数和为0的性质即可求得点A、B的坐标;
(2)①先求得直线AB的解析式,根据![]() 求得
求得![]() ,继而求得点
,继而求得点![]() 的横坐标,从而求得答案;
的横坐标,从而求得答案;
②先求得直线AM的解析式及点![]() 的坐标,过点
的坐标,过点![]() 过
过![]() 轴的平行线交直线
轴的平行线交直线![]() 与点
与点![]() ,过点
,过点![]() 作
作![]() 垂直于
垂直于![]() 的延长线于点
的延长线于点![]() ,求得
,求得![]() ,即
,即![]() 为最小值,即点
为最小值,即点![]() 为所求,求得点
为所求,求得点![]() 的坐标,再求得
的坐标,再求得![]() 的长即可;
的长即可;
(3)先求得直线BD的解析式,设点![]() ,同理求得直线
,同理求得直线![]() 的解析式,求出点
的解析式,求出点![]() 的坐标为
的坐标为![]() ,证得
,证得![]() ,分∠QGE为直角、∠EQG为直角、∠QEG为直角,三种情况分别求解即可.
,分∠QGE为直角、∠EQG为直角、∠QEG为直角,三种情况分别求解即可.
(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
则![]() ,
,
故点A、B的坐标分别为:![]() ,
,
故答案为:![]() ;
;![]() ;
;
(2)①直线![]() 经过点
经过点![]() 和
和![]() 轴上一点
轴上一点![]() ,
,![]() ,
,
∴![]() ,
,
由(1)得:点A、B的坐标分别为:![]() ,则
,则![]() ,
,![]() ,
,
设直线AB的解析式为:![]() ,
,
∴![]()
解得:![]()
∴直线AB的解析式为:![]() ,
,
∵![]()
∴![]()
作![]() ⊥
⊥![]() 轴于
轴于![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的横坐标为
的横坐标为![]() ,
,
又点![]() 在直线AB上,
在直线AB上,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
②由(1)得:点A、B的坐标分别为:![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
设直线AM的解析式为:![]() ,
,
∴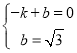
解得: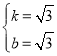
∴直线AM的解析式为:![]() ,
,
根据题意,平移后点![]() ,
,
过点![]() 过
过![]() 轴的平行线交直线
轴的平行线交直线![]() 与点
与点![]() ,过点
,过点![]() 作
作![]() 垂直于
垂直于![]() 的延长线于点
的延长线于点![]() ,如图1,
,如图1,
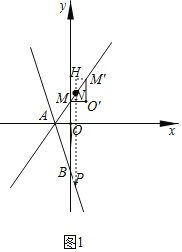
∴![]() ∥
∥![]() ,
,
∵![]() ,
,
∴![]() ,
,
则![]() ,
,
![]() 为最小值,即点
为最小值,即点![]() 为所求,
为所求,
则点N的横坐标与点![]() 的横坐标相同都是
的横坐标相同都是![]() ,
,
点N在直线AM上,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为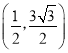 ,
,
∴![]() ,
,
![]() ;
;
(3)根据题意得:
点![]() 的坐标分别为:
的坐标分别为:![]() ,
,
设直线![]() 的解析式为:
的解析式为:![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴直线BD的解析式为:![]() ,
,
设点![]() ,同理直线
,同理直线![]() 的解析式为:
的解析式为:![]() ,
,
∵![]() ,
,
∴设直线![]() 的解析式为:
的解析式为:![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
则直线![]() 的解析式为:
的解析式为:![]() ,
,
故点![]() 的坐标为
的坐标为![]() ,
,
即![]() ,
,
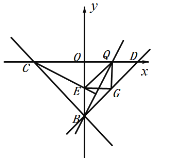
①当![]() 为直角时,
为直角时,
如下图,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
将点![]() 的坐标代入直线
的坐标代入直线![]() 的解析式
的解析式![]() 并解得:
并解得:![]() ,
,
故点![]() ;
;
②当![]() 为直角时,
为直角时,
如下图,作![]() 于
于![]() ,
,
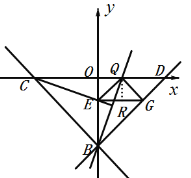
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ∥
∥![]() 轴,
轴,![]() 、
、![]() 和
和![]() 都是底边相等的等腰直角三角形,
都是底边相等的等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
将点![]() 的坐标代入直线
的坐标代入直线![]() 的解析式
的解析式![]() 并解得:
并解得:![]() ,
,
故点![]() ;
;
③当![]() 为直角时,
为直角时,
如下图,
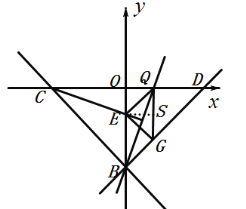
同理可得点![]() 的坐标为
的坐标为![]() ,
,
将点![]() 的坐标代入直线
的坐标代入直线![]() 的解析式
的解析式![]() 并解得:
并解得:![]() ,
,
故点![]() ;
;
综上,点![]() 的坐标为:
的坐标为:![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
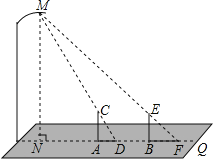
【题目】晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组在创客嘉年华活动中组织了计算机编程比赛,八年级每班派25名学生参加,成绩分别为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级.其中相应等级的得分依次记为10分、9分、8分、7分.将八年级的一班和二班的成绩整理并绘制成如下统计图表:
四个等级.其中相应等级的得分依次记为10分、9分、8分、7分.将八年级的一班和二班的成绩整理并绘制成如下统计图表:
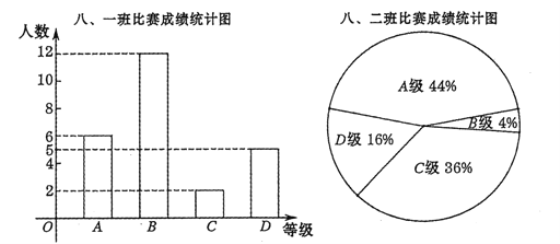
班级 | 平均数(分) | 中位数(分) | 众数(分) | 方差 |
一班 | 8.76 | 9 | 9 |
|
二班 | 8.76 | 8 | 10 |
|
请根据本学期所学过的《数据的分析》相关知识分析上述数据,帮助计算机编程老师选择一个班级参加校级比赛,并阐述你选择的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与 ![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 为直线
为直线 ![]() 上一点,直线
上一点,直线![]()
![]() 过点
过点![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)直线![]() 与
与 ![]() 轴交于点
轴交于点![]() ,动点
,动点 ![]() 在射线
在射线 ![]() 上从点
上从点![]() 开始以每秒 1 个单位的速度运动.设点
开始以每秒 1 个单位的速度运动.设点 ![]() 的运动时间为
的运动时间为![]() 秒;
秒;
①若![]() 的面积为
的面积为![]() ,请求出
,请求出![]() 与
与 ![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 ![]() 的取值范围;
的取值范围;
②是否存在 ![]() 的值,使得
的值,使得 ![]() ?若存在,请求出
?若存在,请求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列满足条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3B.三内角之比为3:4:5
C.三边之比为3:4:5D.三边之比为5:12:13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB的高为16m,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为 60°,在楼顶B处测得塔顶D处的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求塔CD的高.(![]() =1.73,结果保留一位小数.)
=1.73,结果保留一位小数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
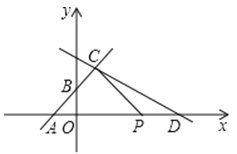
【题目】如图,已知函数 y=x+1 的图象与 y 轴交于点 A,一次函数 y=kx+b 的图象经过点 B(0,﹣1),与x 轴 以及 y=x+1 的图象分别交于点 C、D,且点 D 的坐标为(1,n),

(1)则n= ,k= ,b= ;
(2)函数 y=kx+b 的函数值大于函数 y=x+1 的函数值,则X的取值范围是 ;
(3)求四边形 AOCD 的面积;
(4)在 x轴上是否存在点 P,使得以点 P,C,D 为顶点的三角形是直角三角形?若存在求出点 P 的坐标; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 为
为![]() 上两点,且
上两点,且![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.

(1)如图1,当![]() 两点重合时,求证:
两点重合时,求证:![]() ;
;
(2)延长![]() 与
与![]() 交于点
交于点![]() .
.
①如图2,求证:![]() ;
;
②如图3,连接![]() ,若
,若![]() ,则
,则![]() 的面积为______________.
的面积为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com