
 ��ͼ��ƽ��ֱ������ϵ�У�ֱ��AB��y=-$\frac{1}{3}$x+b��y���ڵ�A��0��1������x���ڵ�B������E��1��0����x��Ĵ���EF��AB�ڵ�D��P��ֱ��EF��һ���㣬���ڵ�D���Ϸ�����P��1��n����
��ͼ��ƽ��ֱ������ϵ�У�ֱ��AB��y=-$\frac{1}{3}$x+b��y���ڵ�A��0��1������x���ڵ�B������E��1��0����x��Ĵ���EF��AB�ڵ�D��P��ֱ��EF��һ���㣬���ڵ�D���Ϸ�����P��1��n�������� ��1����A���������ֱ��AB�Ľ���ʽ���������b��ֵ��
��2������A��AM��PD������ΪM�����AM�ij���������á�BPD�͡�PAB����������ߵĺͼ�����ã�
��3����S��ABP=2ʱ��$\frac{3}{2}$n-1=2�����n=2�����OBP=45�㣬Ȼ���A��B��P�ֱ���ֱ�Ƕ�����⣮
��� �⣺��1����y=-$\frac{1}{3}$x+b����A��0��1����
��b=1��
��ֱ��AB�Ľ���ʽ��y=-$\frac{1}{3}$x+1��
�ʴ�Ϊ��y=-$\frac{1}{3}$x+1��
��2������A��AM��PD������ΪM������AM=1����x=1ʱ��y=-$\frac{1}{3}$x+1=$\frac{2}{3}$��P�ڵ�D���Ϸ���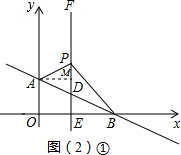
��PD=n-$\frac{2}{3}$��S${\;}_{��APD}=\frac{1}{2}$PD•AM=$\frac{1}{2}��1����n-\frac{2}{3}��=\frac{1}{2}n-\frac{1}{3}$��
�ɵ�B��3��0������֪��B��ֱ��x=1�ľ���Ϊ2������BDP�ı�PD�ϵĸ߳�Ϊ2��
��S��BPD=$\frac{1}{2}$PD��2=n-$\frac{2}{3}$��
��S��PAB=S��APD+S��BPD=$\frac{1}{2}$n-$\frac{1}{3}$+n-$\frac{2}{3}$=$\frac{3}{2}$n-1��
��3����S��ABP=2ʱ��$\frac{3}{2}$n-1=2�����n=2��
���P��1��2����
��E��1��0����
��PE=BE=2��
���EPB=��EBP=45�㣮
��1���������ͼ1����CPB=90�㣬BP=PC��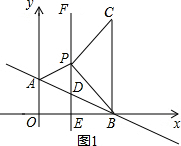
����C��CN��ֱ��x=1�ڵ�N��
�ߡ�CPB=90�㣬��EPB=45�㣬
���NPC=��EPB=45�㣬
�ڡ�CNP���BEP�У�$\left\{\begin{array}{l}{��NPC=��EPB}\\{��CNP=��PEB=90��}\\{BP=PC}\end{array}\right.$��
���CNP�ա�BEP��
��PN=NC=EB=PE=2��
��NE=NP+PE=2+2=4��
��C��3��4����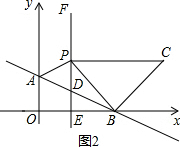
��2���������ͼ2��PBC=90�㣬BP=BC��
����C��CF��x���ڵ�F��
�ߡ�PBC=90�㣬��EBP=45�㣬
���CBF=��PBE=45�㣬
�ڡ�CBP���PBE�У�$\left\{\begin{array}{l}{��CBF=��PBE}\\{��CFB=��PEB}\\{BC=BP}\end{array}\right.$��
���CBF�ա�PBE��
��BF=CF=PE=EB=2��
��OF=OB+BF=3+2=5��
��C��5��2����
��3���������ͼ3����PCB=90�㣬CP=EB��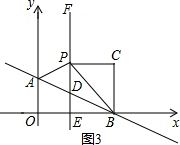
���CPB=��EBP=45�㣬
�ڡ�PCB�͡�PEB�У�
$\left\{\begin{array}{l}{CP=EB}\\{��CPB=��EBP}\\{BP=BP}\end{array}\right.$��
���PCB�ա�PEB��SAS����
��PC=CB=PE=EB=2��
��C��3��2����
����PBΪ���ڵ�һ����������ֱ��������BPC����C�������ǣ�3��4����5��2����3��2����
���� ���⿼���˴���ϵ���������Ľ���ʽ��ȫ�������ε��ж������ʣ�����ֱ�������ε����ʵ��ۺ�Ӧ�ã���ȷ���n��ֵ���жϡ�OBP=45���ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ijУ���꼶�ԡ�����ϲ���������˶���Ϊ����Ը�У���꼶ÿλѧ�������˵��飬������˶���Ŀ�У�������ë��ƹ����������������Ŀ��ÿλͬѧ��ѡһ���������ÿλͬѧ������ѡ���ݵ�������������ͳ��ͼ����
ijУ���꼶�ԡ�����ϲ���������˶���Ϊ����Ը�У���꼶ÿλѧ�������˵��飬������˶���Ŀ�У�������ë��ƹ����������������Ŀ��ÿλͬѧ��ѡһ���������ÿλͬѧ������ѡ���ݵ�������������ͳ��ͼ����| �˶���Ŀ | Ƶ�� |
| ���� | 90 |
| ��� | m |
| ƹ���� | 108 |
| ���� | 54 |
| ���� | n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ���������ƽ��չ��ͼ�����۳��������ÿ��������ϱ�ע��ֵ�ĺ;���ȣ���x+y=10��
��ͼ��һ���������ƽ��չ��ͼ�����۳��������ÿ��������ϱ�ע��ֵ�ĺ;���ȣ���x+y=10���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 23 | B�� | 19 | C�� | 29 | D�� | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2012��1+x��2=2014 | B�� | 2845��1+x��2=3112 | C�� | 3112��1+x��2=2845 | D�� | 2845��1-x��2=3112 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com