
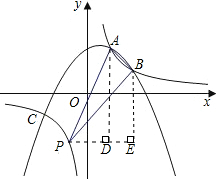
 如图,抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和C(-2,-1)三点.
如图,抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和C(-2,-1)三点. 的图象的一个分支经过点C,并且另个分支与抛物线在第一象限相交.
的图象的一个分支经过点C,并且另个分支与抛物线在第一象限相交. 的图象是否经过点A和点B,试说明理由;
的图象是否经过点A和点B,试说明理由; 在第三象限的图象上的一个动点,连接AB、PA、PB,请问是否存在这样的一点P使△PAB的面积为3?如果存在,试求出所有符合条件的点P的坐标;如果不存在,请说明理由.
在第三象限的图象上的一个动点,连接AB、PA、PB,请问是否存在这样的一点P使△PAB的面积为3?如果存在,试求出所有符合条件的点P的坐标;如果不存在,请说明理由.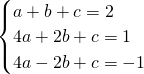
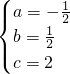
 x2+
x2+ +2
+2 的图象的一个分支经过点C(-2,-1)
的图象的一个分支经过点C(-2,-1) ,
, 的图象上,
的图象上, 的图象上,
的图象上, 的图象经过点A和点B,
的图象经过点A和点B, 上,
上, )
) +2,BE=-
+2,BE=- +1
+1 AD•PD=
AD•PD= (-
(- +2)(-a+1)=-a-
+2)(-a+1)=-a- +2
+2 (AD+BE)•DE=
(AD+BE)•DE= -
-
 PE•BE=-
PE•BE=- a-
a- +2
+2 a-
a- +
+
 a-
a- +
+ =3
=3 a-
a- +
+ =3的解
=3的解 ;②由k的值等于2,若A,B两点的横纵坐标相乘等于2,则反比例函数就经过该点.③直接求△PAB的面积不容易,可以过P作PE∥x轴,作AD⊥PE于D,BE⊥PE于E,先求出四边形ABEP的面积,再减去△BPE的面积,即得△PAB的面积,令其等于3,即可求得满足条件的点P.
;②由k的值等于2,若A,B两点的横纵坐标相乘等于2,则反比例函数就经过该点.③直接求△PAB的面积不容易,可以过P作PE∥x轴,作AD⊥PE于D,BE⊥PE于E,先求出四边形ABEP的面积,再减去△BPE的面积,即得△PAB的面积,令其等于3,即可求得满足条件的点P.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 9 |
| 8 |
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
 O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1.查看答案和解析>>
科目:初中数学 来源: 题型:
 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12,查看答案和解析>>
科目:初中数学 来源: 题型:
 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com