ÒŃÖȘĆŚÎïÏßy=ax
2+bx+6ÓëxÖ᜻ÓÚAĄąBÁœ”㣚”ăAÔÚÔ”ă”ÄŚóČàŁŹ”ăBÔÚÔ”ă”ÄÓÒČàŁ©ŁŹÓëyÖ᜻ÓÚ”ăCŁŹÇÒOB=
OCŁŹtanĄÏACO=
ŁŹ¶„”ăÎȘDŁź
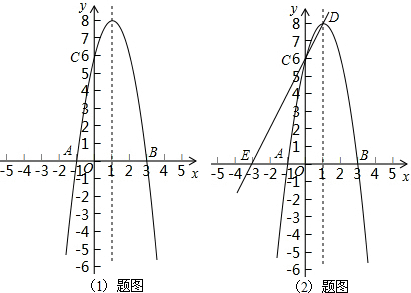
Łš1Ł©Çó”ăA”ÄŚű±êŁź
Łš2Ł©ÇóÖ±ÏßCDÓëxÖá”Äœ»”ăE”ÄŚű±êŁź
Łš3Ł©ÔÚŽËĆŚÎïÏßÉÏÊÇ·ńŽæÔÚÒ»”ăFŁŹÊč”ĂÒÔ”ăAĄąCĄąEĄąFÎȘ¶„”ă”ÄËıßĐÎÊÇÆœĐĐËıßĐÎŁżÈôŽæÔÚŁŹÇëÇółö”ăF”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź
Łš4Ł©Èô”ăMŁš2ŁŹyŁ©ÊÇŽËĆŚÎïÏßÉÏÒ»”㣏”ăNÊÇÖ±ÏßAMÉÏ·œ”ÄĆŚÎïÏßÉÏÒ»¶Ż”㣏”±”ăNÔ˶Ż”œÊČÎλÖĂʱŁŹËıßĐÎABMN”ÄĂæ»ęSŚîŽóŁżÇëÇółöŽËʱS”ÄŚîŽóÖ”șÍ”ăN”ÄŚű±êŁź
Łš5Ł©”ăPÎȘŽËĆŚÎïÏ߶ԳÆÖáÉÏÒ»¶Ż”㣏ÈôÒÔ”ăPÎȘÔČĐÄ”ÄÔČÓ룚4Ł©ÖĐ”ÄÖ±ÏßAMŒ°xÖáÍŹÊ±ÏàÇĐŁŹÔòŽËʱ”ăP”ÄŚű±êÎȘ
Łź



 ĄàDŁš1ŁŹ8Ł©ŁŹ
ĄàDŁš1ŁŹ8Ł©ŁŹ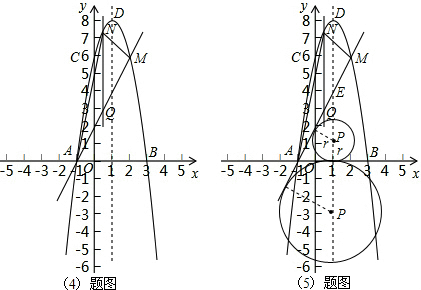



 ÓëxÖá”ÄÁíÒ»žöœ»”ăÎȘEŁź
ÓëxÖá”ÄÁíÒ»žöœ»”ăÎȘEŁź ÈçÍŒŁŹÒŃÖȘĆŚÎïÏßy=ax2+bx+cŁšÆäÖĐbŁŸ0ŁŹcŁŒ0Ł©”Ķ„”ăPÔÚxÖáÉÏŁŹÓëyÖ᜻ÓÚ”ăQŁŹčęŚű±êÔ”ăOŁŹŚśOAĄÍPQŁŹŽčŚăÎȘAŁŹÇÒOA=
ÈçÍŒŁŹÒŃÖȘĆŚÎïÏßy=ax2+bx+cŁšÆäÖĐbŁŸ0ŁŹcŁŒ0Ł©”Ķ„”ăPÔÚxÖáÉÏŁŹÓëyÖ᜻ÓÚ”ăQŁŹčęŚű±êÔ”ăOŁŹŚśOAĄÍPQŁŹŽčŚăÎȘAŁŹÇÒOA=