
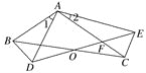
【题目】如图,△ABC≌△ADE且∠ABC=∠ADE,∠ACB=∠AED,BC、DE交于点O.则下列四个结论中,①∠1=∠2;②BC=DE;③△ABD∽△ACE;④A、O、C、E四点在同一个圆上,一定成立的有( )
A. 1个
B. 2个
C. 3个
D. 4个
【答案】D
【解析】
由△ABC≌△ADE且∠ABC=∠ADE,∠ACB=∠AED,根据全等三角形的性质,即可求得BC=DE,∠BAC=∠DAE,继而可得∠1=∠2,则可判定①②正确;由△ABC≌△ADE,可得AB=AD,AC=AE,则可得AB:AC=AD:AE,根据有两边对应成比例且夹角相等三角形相似,即可判定③正确;易证得△AEF∽△OCF与△AOF∽△CEF,继而可得∠OAE+∠OCE=180°,即可判定A、O、C、E四点在同一个圆上.

∵△ABC≌△ADE且∠ABC=∠ADE,∠ACB=∠AED,
∴∠BAC=∠DAE,BC=DE,故②正确;
∴∠BAC∠DAC=∠DAE∠DAC,
即∠1=∠2,故①正确;
∵△ABC≌△ADE,
∴AB=AD,AC=AE,
∴![]() =
=![]() ,
,
∵∠1=∠2,
∴△ABD∽△ACE,故③正确;
∵∠ACB=∠AEF,∠AFE=∠OFC,
∴△AFE∽△OFC,
∴![]() =
=![]() ,∠2=∠FOC,
,∠2=∠FOC,
即![]() =
=![]() ,
,
∵∠AFO=∠EFC,
∴△AFO∽△EFC,
∴∠FAO=∠FEC,
∴∠EAO+∠ECO=∠2+∠FAO+∠ECO=∠FOC+∠FEC+∠ECO=180![]() ,
,
∴A、O、C.E四点在同一个圆上,故④正确。
故选D.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】某民俗村为了维护消费者利益,限定村内所有商品的利润率不得超过![]() ,村内一商店以每件16元的价格购进一批商品,该商品每件售价定为x元,每天可卖出
,村内一商店以每件16元的价格购进一批商品,该商品每件售价定为x元,每天可卖出![]() 件,每天销售该商品所获得的利润为y元.
件,每天销售该商品所获得的利润为y元.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 若每天销售该商品要获得280元的利润,每件商品的售价应定为多少元?
若每天销售该商品要获得280元的利润,每件商品的售价应定为多少元?
![]() 求商店每天销售该商品可获得的最大利润.
求商店每天销售该商品可获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
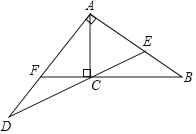
【题目】如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求∠D的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线l1:y=(x﹣2)2﹣4与x轴分别交于O、A两点,将抛物线l1向上平移得到l2,过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为12,则抛物线l2的函数表达式为( )
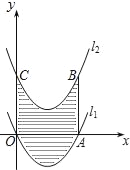
A. y=(x﹣2)2﹣1 B. y=(x﹣2)2+1 C. y=(x﹣2)2﹣2 D. y=(x﹣2)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
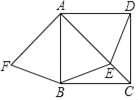
【题目】如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)BF和DE有怎样的数量关系?请证明你的结论;
(2)在其他条件都保持不变的是情况下,当点E运动到AC中点时,四边形AFBE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
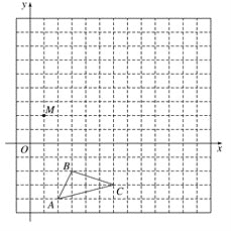
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2∶1.
(3)求出A2B2、C2三点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
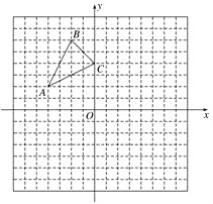
【题目】如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系平面上三点.
(1)把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1,画出平移后的图形;
(2)若△ABC内部有一点P(a,b),则平移后它的对应点P1的坐标为__________;
(3)以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2,请在所给的坐标系中作出所有满足条件的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
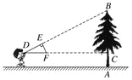
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50 cm,EF=25 cm,测得边DF离地面的高度AC=1.6 m,CD=10 m,则树高AB等于( )
A. 4 m
B. 5 m
C. 6.6 m
D. 7.7 m
查看答案和解析>>
科目:初中数学 来源: 题型:
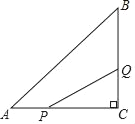
【题目】如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P从点A沿AC向C以2cm/s的速度移动,到C即停,点Q从点C沿CB向B以1cm/s的速度移动,到B就停.
(1)若P、Q同时出发,经过几秒钟S△PCQ=2cm2;
(2)若点Q从C点出发2s后点P从点A出发,再经过几秒△PCQ与△ACB相似.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com