
【题目】如图,半径为1的![]() 与
与![]() 轴交于
轴交于![]() 两点,圆心
两点,圆心![]() 的坐标为
的坐标为![]() ,二次函数
,二次函数![]() 的图象经过
的图象经过![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求二次函数的解析式.
(2)经过坐标原点![]() 的直线
的直线![]() 与
与![]() 相切,求直线
相切,求直线![]() 的解析式.
的解析式.
(3)试问在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)将点A,B的坐标代入函数表达式,解出b,c的值即可;
(2)设直线![]() 与
与![]() 相切于点
相切于点![]() ,求出OE的长,过点
,求出OE的长,过点![]() 作
作![]() 轴于点
轴于点![]() ,可得比例式
,可得比例式![]() ,可求出EH的长度,从而求出OH,即点E坐标,可得l的解析式,再根据两条直线关于x轴对称可得另一条直线的表达式;
,可求出EH的长度,从而求出OH,即点E坐标,可得l的解析式,再根据两条直线关于x轴对称可得另一条直线的表达式;
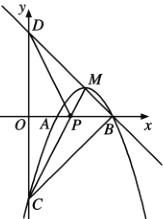
(3)利用轴对称的应用,当△PMD的周长取最小值时,求出M点的坐标,设直线![]() 的
的
解析式为![]() ,根据点B的坐标求出BM解析式,得到点D坐标,可知点D与点C坐标关于x轴对称,连接
,根据点B的坐标求出BM解析式,得到点D坐标,可知点D与点C坐标关于x轴对称,连接![]() ,设直线
,设直线![]() 的解析式为
的解析式为![]() ,将C,M的坐标代入,则CM与x轴交点即为点P的坐标.
,将C,M的坐标代入,则CM与x轴交点即为点P的坐标.
解:(1)由题意可知![]() ,
,
![]() 二次函数
二次函数![]() 的图象经过
的图象经过![]() 两点,
两点,
![]() ,
,
解得![]() ,
,
![]() 二次函数的解析式
二次函数的解析式![]()
(2)如图,设直线![]() 与
与![]() 相切于点
相切于点![]() ,
,
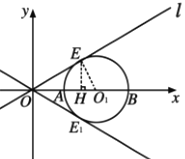
![]()
![]()
过点![]() 作
作![]() 轴于点
轴于点![]()
![]()
![]()
![]() ,
,
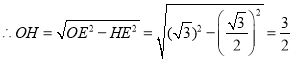 ,
,
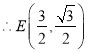 ,
,
![]() 的解析式为
的解析式为![]() ,
,
根据对称性,满足条件的另一条直线的解析式为![]() ,
,
![]() 所求直线
所求直线![]() 的解析式为:
的解析式为:![]() 或
或![]() .
.
(3)存在
理由:![]() 为二次函数
为二次函数![]() 的顶点,
的顶点,
![]() ,
,
![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
![]() 点
点![]() 坐标为
坐标为![]() ,
,
![]() ,
,
解得![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
![]() 直线
直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,
![]() 点
点![]() 与
与![]() 关于
关于![]() 轴对称,
轴对称,
连接![]() ,设直线
,设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得,
代入得,
![]() ,
,
解得![]() ,
,
![]() ,
,
直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:①b2﹣4ac=0 ②a+b+c>0 ③2a﹣b=0④c﹣a=3,其中正确的有_____.(填序号)
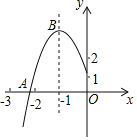
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC
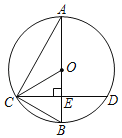
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是( )

A.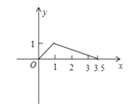 B.
B.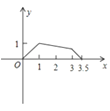 C.
C.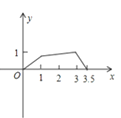 D.
D.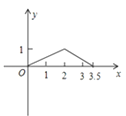
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3经过点 B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.
(1)求抛物线的表达式;
(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)
(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;
(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古贤常说万物皆自然,而古希腊学者说万物皆数.同学们还记得我们最初接触的数就是“自然数”吧!在数的学习过程中,我们会对其中一些具有某种特性的自然数进行研究,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“![]() 喜数”.
喜数”.
定义:对于一个两位自然数,如果它的个位和十位上的数字均不为零,且它正好等于其个位和十位上的数字的和的![]() 倍(
倍(![]() 为正整数),我们就说这个自然数是一个“
为正整数),我们就说这个自然数是一个“![]() 喜数”.
喜数”.
例如:24就是一个“4喜数”,因为![]()
25就不是一个“![]() 喜数”因为
喜数”因为![]()
(1)判断44和72是否是“![]() 喜数”?请说明理由;
喜数”?请说明理由;
(2)试讨论是否存在“7喜数”若存在请写出来,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB为⊙O的一条弦,以AB为直角边作等腰直角△ABC,直线AC恰好是⊙O的切线,点D为⊙O上的一点,连接DA,DB,DC,若DA=3,DB=4,则DC的长为_____.
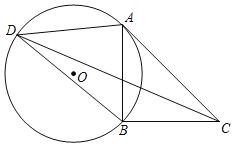
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:
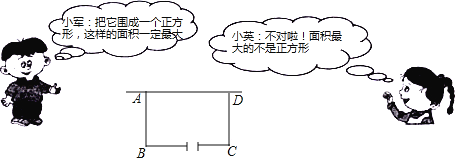
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李师傅驾驶出租车匀速地从西安市送客到咸阳国际机场,全程约![]() ,设小汽车的行驶时间为
,设小汽车的行驶时间为![]() (单位:
(单位:![]() ),行驶速度为
),行驶速度为![]() (单位:
(单位:![]() ),且全程速度限定为不超过
),且全程速度限定为不超过![]() .
.
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)李师傅上午![]() 点驾驶小汽车从西安市出发.需在
点驾驶小汽车从西安市出发.需在![]() 分钟后将乘客送达咸阳国际机场,求小汽车行驶速度
分钟后将乘客送达咸阳国际机场,求小汽车行驶速度![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com