
【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=![]() +bx+c经过A. B两点,与y轴交于点D(0,6).
+bx+c经过A. B两点,与y轴交于点D(0,6).
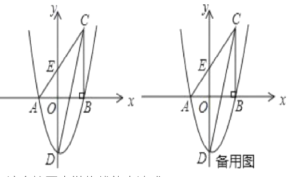
(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由。
【答案】(1)![]() ;(2)DE=
;(2)DE=![]() +6=
+6=![]() ;(3)S=
;(3)S=![]() (2<m<4);(4)N点坐标为(
(2<m<4);(4)N点坐标为(![]() );(
);( ![]() )
)
【解析】
(1)先确定B(4,0),再利用待定系数法求出抛物线解析式为![]()
(2)先利用待定系数法求得直线AC的解析式为y=![]() ,则可确定E(0,
,则可确定E(0,![]() ),然后计算DE的长;
),然后计算DE的长;
(3)如图1,作PQ∥y轴交AC于Q,设P(m,![]() -6),则Q(m,
-6),则Q(m,![]() ),则PQ=-
),则PQ=-![]() ,然后根据三角形面积公式,利用S=S△PAQ+S△PCQ计算即可;
,然后根据三角形面积公式,利用S=S△PAQ+S△PCQ计算即可;
(4)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,根据角平分线的性质得FH=FB,易得AH=AB=6,再利用∠ACB的余弦可求出CF=5,则F(4,3),接着求出直线AF的解析式为y=![]() x+1,于是通过解方程组
x+1,于是通过解方程组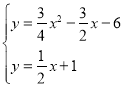 得N点坐标为(
得N点坐标为(![]() );当点M′在x的负半轴上时,AN′交y轴与G,先在证明Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组
);当点M′在x的负半轴上时,AN′交y轴与G,先在证明Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组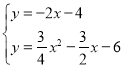 得N的坐标.
得N的坐标.
(1)∵BC⊥x轴,点C(4,8),
∴B(4,0),
把B(4,0),C(0,6)代入y=![]() +bx+c得
+bx+c得![]() ,解得
,解得 ,
,
∴抛物线解析式为![]() ;
;
(2)设直线AC的解析式为y=px+q,
把A(2,0),C(4,8)代入得![]() ,解得
,解得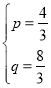 ,
,
∴直线AC的解析式为y=![]() ,
,
当x=0时,y=![]() =
=![]() ,则E(0,
,则E(0, ![]() ),
),
∴DE=![]() +6=
+6=![]() ;
;
(3)如图1,作PQ∥y轴交AC于Q,
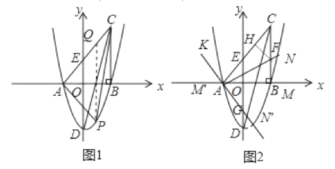
设P(m,![]() -6),则Q(m,
-6),则Q(m,![]() ),
),
∴PQ=-![]() ,
,
∴S=S△PAQ+S△PCQ=![]() 6PQ=
6PQ=![]() (2<m<4);
(2<m<4);
(4)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,则FH=FB,
易得AH=AB=6,
∵AC=![]() =
=![]() =10,
=10,
∴CH=106=4,
∵cos∠ACB=![]() ,
,
∴CF=![]() =5,
=5,
∴F(4,3),
易得直线AF的解析式为y=![]() x+1,
x+1,
解方程组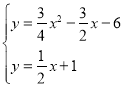 得
得![]() 或
或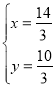 ,
,
∴N点坐标为(![]() );
);
当点M′在x的负半轴上时,AN′交y轴与G,
∵∠CAN′=∠M′AN′,
∴∠KAM′=∠CAK,
而∠CAN=∠MAN,
∴∠KAC+∠CAN=90°,
而∠MAN+∠AFB=90°,
∴∠KAC=∠AFB,
而∠KAM′=∠GAO,
∴∠GAO=∠AFB,
∴Rt△OAG∽Rt△BFA,
∴![]() ,即
,即![]() ,解得OG=4,
,解得OG=4,
∴G(0,4),
易得直线AG的解析式为y=2x4,
解方程组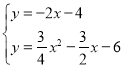 得
得![]() 或
或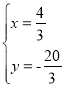 ,
,
∴N′的坐标为(![]() ),
),
综上所述,满足条件的N点坐标为(![]() );(
);( ![]() )
)


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,几秒种后△DPQ的面积为31cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
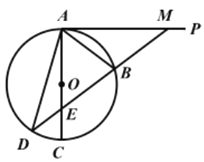
【题目】如图,AC是⊙O的一条弦,AP是⊙O的切线。作BM=AB并与AP交于点M,延长MB交AC于点E,交⊙O于点D,连接AD.
(1)求证:AB=BE;
(2)若⊙O的半径R=5,AB=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车油箱中有汽油![]() .如果不再加油,那么油箱中的油量
.如果不再加油,那么油箱中的油量![]() (单位:
(单位:![]() )随行驶路程
)随行驶路程![]() (单位:
(单位:![]() )的增加而减少.已知该汽车平均耗油量为
)的增加而减少.已知该汽车平均耗油量为![]() .
.
(Ⅰ)计算并填写下表:
| 10 | 100 | 300 | … |
| … |
(Ⅱ)写出表示![]() 与
与![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,
,![]() 两地的路程约有
两地的路程约有![]() ,当油箱中油量少于
,当油箱中油量少于![]() 时,汽车会自动报警,则这辆汽车在由
时,汽车会自动报警,则这辆汽车在由![]() 地到
地到![]() 地,再由
地,再由![]() 地返回
地返回![]() 地的往返途中,汽车是否会报警?请说明理由.
地的往返途中,汽车是否会报警?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)求甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2000元,那么最多可购买多少个甲礼品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一,抛物线![]() 过
过![]() 三点
三点
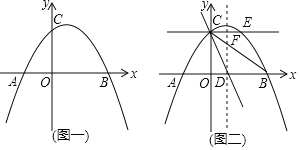
(1)求该抛物线的解析式;
(2)![]() 两点均在该抛物线上,若
两点均在该抛物线上,若![]() ,求
,求![]() 点横坐标
点横坐标![]() 的取值范围;
的取值范围;
(3)如图二,过点![]() 作
作![]() 轴的平行线交抛物线于点
轴的平行线交抛物线于点![]() ,该抛物线的对称轴与
,该抛物线的对称轴与![]() 轴交于点
轴交于点![]() ,连结
,连结![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 分别为直线
分别为直线![]() 和
和![]() 上的动点,求
上的动点,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,A、B均为格点.
(I).![]() 的长等于_________;
的长等于_________;
(II).请用无刻度的直尺,在如图所示的网格中求作一点![]() ,使得以
,使得以![]() 为底边的等腰三角形
为底边的等腰三角形![]() 的面积等于
的面积等于![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明);_____________
的位置是如何找到的(不要求证明);_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应地任务:
莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则![]() .
.
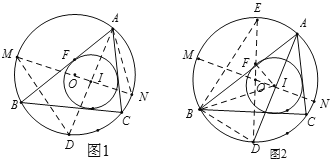
如图1,⊙O和⊙I分别是△ABC的外接圆和内切圆,⊙I与AB相切分于点F,设⊙O的半径为R,⊙I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有d2=R2﹣2Rr.
下面是该定理的证明过程(部分):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI,
∴![]() ,
,
∴![]() ①,
①,
如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF,
∵DE是⊙O的直径,∴∠DBE=90°,
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA,
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB,
∴![]() ,∴
,∴![]() ②,
②,
任务:(1)观察发现:![]() ,
,![]() (用含R,d的代数式表示);
(用含R,d的代数式表示);
(2)请判断BD和ID的数量关系,并说明理由;
(3)请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;
(4)应用:若△ABC的外接圆的半径为5cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离为 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作![]() 两种手工艺品,
两种手工艺品,![]() 每天每件获利比
每天每件获利比![]() 多105元,获利30元的
多105元,获利30元的![]() 与获利240元的
与获利240元的![]() 数量相等.
数量相等.
(1)制作一件![]() 和一件
和一件![]() 分别获利多少元?
分别获利多少元?
(2)工厂安排65人制作![]() ,
,![]() 两种手工艺品,每人每天制作2件
两种手工艺品,每人每天制作2件![]() 或1件
或1件![]() .现在在不增加工人的情况下,增加制作
.现在在不增加工人的情况下,增加制作![]() .已知每人每天可制作1件
.已知每人每天可制作1件![]() (每人每天只能制作一种手工艺品),要求每天制作
(每人每天只能制作一种手工艺品),要求每天制作![]() ,
,![]() 两种手工艺品的数量相等.设每天安排
两种手工艺品的数量相等.设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)在(1)(2)的条件下,每天制作![]() 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知
不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知![]() 每件获利30元,求每天制作三种手工艺品可获得的总利润
每件获利30元,求每天制作三种手工艺品可获得的总利润![]() (元)的最大值及相应
(元)的最大值及相应![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com