
如图所示,在Rt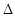 ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为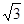 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt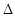 ABC绕A点顺时针旋转120°后得到Rt
ABC绕A点顺时针旋转120°后得到Rt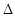 ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.
(1)画出旋转后的Rt ADE,求出Rt
ADE,求出Rt ADE
的直角边DE被⊙M截得的弦PQ的长度;
ADE
的直角边DE被⊙M截得的弦PQ的长度;
(2)判断Rt ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
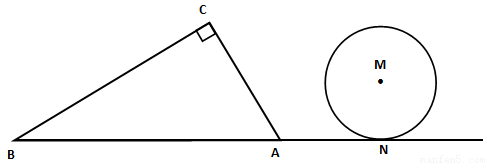
(1)解:如图所示 ,过M作MF⊥PQ于F,连接MP
MF=NE=AE-AN=AC-AN=4-3=1
在Rt△PFM中, PM2= PF2 +FM2
PF=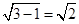
PQ=2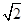
(2) AD与⊙M相切.
证明:过点M作MH⊥AD于H,连接MN,MA,则MN⊥AE,且MN= 3 ,

在Rt△AMN中,tan∠MAN=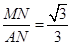 ,
,
∴∠MAN=30°,
∵∠DAE=∠BAC=60°,
∴∠MAD=30°,
∴∠MAN=∠MAD=30°,
∴MH=MN,
∴AD与⊙M相切.
【解析】(1)把三角形AB旋转120°就能得到图形.
(2)连接MQ,过M点作MF⊥DE,由AN=3,AC=4,求出NE的长;在Rt△MFQ中,利用勾股定理可求出QF,根据垂径定理知QF就是弧长PQ的一半.
(3)过M作AD的垂线设垂足为H,然后证MH与⊙M半径的大小关系即可;连接AM、MN,由于AE是⊙M的切线,故MN⊥AE,在Rt△AMN中,通过解直角三角形,易求得∠MAN=30°,由此可证得AM是∠DAE的角平分线,根据角平分线的性质即可得到MH=MN,由此可证得⊙M与AD相切.


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源:2012届浙江省温岭市三校联考九年级上学期第二次学业水平考试数学试卷(带解析) 题型:解答题
如图所示,在Rt ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为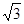 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt ABC绕A点顺时针旋转120°后得到Rt
ABC绕A点顺时针旋转120°后得到Rt ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.
(1)画出旋转后的Rt ADE,求出Rt
ADE,求出Rt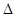 ADE 的直角边DE被⊙M截得的弦PQ的长度;
ADE 的直角边DE被⊙M截得的弦PQ的长度;
(2)判断Rt ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com