
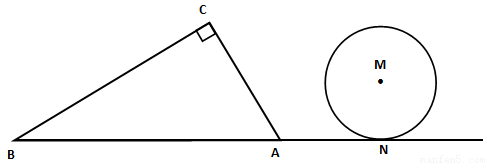
如图所示,在Rt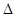 ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为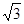 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt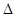 ABC绕A点顺时针旋转120°后得到Rt
ABC绕A点顺时针旋转120°后得到Rt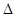 ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.
(1)画出旋转后的Rt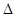 ADE,求出Rt
ADE,求出Rt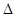 ADE 的直角边DE被⊙M截得的弦PQ的长度;
ADE 的直角边DE被⊙M截得的弦PQ的长度;
(2)判断Rt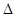 ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)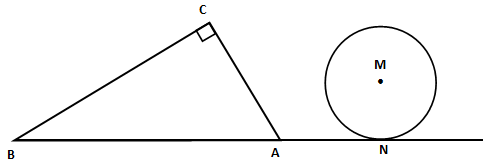
科目:初中数学 来源:2011-2012学年浙江省温岭市三校联考九年级上学期第二次学业水平考试数学试卷(解析版) 题型:解答题
如图所示,在Rt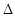 ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为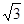 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt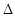 ABC绕A点顺时针旋转120°后得到Rt
ABC绕A点顺时针旋转120°后得到Rt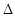 ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.
(1)画出旋转后的Rt ADE,求出Rt
ADE,求出Rt ADE
的直角边DE被⊙M截得的弦PQ的长度;
ADE
的直角边DE被⊙M截得的弦PQ的长度;
(2)判断Rt ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com