
【题目】已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b.
(Ⅰ)求抛物线顶点Q的坐标(用含a的代数式表示);
(Ⅱ)说明直线与抛物线有两个交点;
(Ⅲ)直线与抛物线的另一个交点记为N.
(ⅰ)若﹣1≤a≤﹣ ![]() ,求线段MN长度的取值范围;
,求线段MN长度的取值范围;
(ⅱ)求△QMN面积的最小值.
【答案】解:(Ⅰ)∵抛物线y=ax2+ax+b过点M(1,0),
∴a+a+b=0,即b=﹣2a,
∴y=ax2+ax+b=ax2+ax﹣2a=a(x+ ![]() )2﹣
)2﹣ ![]() ,
,
∴抛物线顶点Q的坐标为(﹣ ![]() ,﹣
,﹣ ![]() );
);
(Ⅱ)∵直线y=2x+m经过点M(1,0),
∴0=2×1+m,解得m=﹣2,
联立直线与抛物线解析式,消去y可得ax2+(a﹣2)x﹣2a+2=0(*)
∴△=(a﹣2)2﹣4a(﹣2a+2)=9a2﹣12a+4,
由(Ⅰ)知b=﹣2a,且a<b,
∴a<0,b>0,
∴△>0,
∴方程(*)有两个不相等的实数根,
∴直线与抛物线有两个交点;
(Ⅲ)联立直线与抛物线解析式,消去y可得ax2+(a﹣2)x﹣2a+2=0,即x2+(1﹣ ![]() )x﹣2+
)x﹣2+ ![]() =0,
=0,
∴(x﹣1)[x﹣( ![]() ﹣2)]=0,解得x=1或x=
﹣2)]=0,解得x=1或x= ![]() ﹣2,
﹣2,
∴N点坐标为( ![]() ﹣2,
﹣2, ![]() ﹣6),
﹣6),
(i)由勾股定理可得MN2=[( ![]() ﹣2)﹣1]2+(
﹣2)﹣1]2+( ![]() ﹣6)2=
﹣6)2= ![]() ﹣
﹣ ![]() +45=20(
+45=20( ![]() ﹣
﹣ ![]() )2 ,
)2 ,
∵﹣1≤a≤﹣ ![]() ,
,
∴﹣2≤ ![]() ≤﹣1,
≤﹣1,
∴MN2随 ![]() 的增大而减小,
的增大而减小,
∴当 ![]() =﹣2时,MN2有最大值245,则MN有最大值7
=﹣2时,MN2有最大值245,则MN有最大值7 ![]() ,
,
当 ![]() =﹣1时,MN2有最小值125,则MN有最小值5
=﹣1时,MN2有最小值125,则MN有最小值5 ![]() ,
,
∴线段MN长度的取值范围为5 ![]() ≤MN≤7
≤MN≤7 ![]() ;
;
(ii)如图,设抛物线对称轴交直线与点E,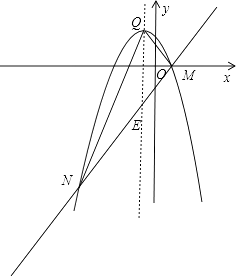
∵抛物线对称轴为x=﹣ ![]() ,
,
∴E(﹣ ![]() ,﹣3),
,﹣3),
∵M(1,0),N( ![]() ﹣2,
﹣2, ![]() ﹣6),且a<0,设△QMN的面积为S,
﹣6),且a<0,设△QMN的面积为S,
∴S=S△QEN+S△QEM= ![]() |(
|( ![]() ﹣2)﹣1||﹣
﹣2)﹣1||﹣ ![]() ﹣(﹣3)|=
﹣(﹣3)|= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ,
,
∴27a2+(8S﹣54)a+24=0(*),
∵关于a的方程(*)有实数根,
∴△=(8S﹣54)2﹣4×27×24≥0,即(8S﹣54)2≥(36 ![]() )2 ,
)2 ,
∵a<0,
∴S= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() >
> ![]() ,
,
∴8S﹣54>0,
∴8S﹣54≥36 ![]() ,即S≥
,即S≥ ![]() +
+ ![]() ,
,
当S= ![]() +
+ ![]() 时,由方程(*)可得a=﹣
时,由方程(*)可得a=﹣ ![]() 满足题意,
满足题意,
∴当a=﹣ ![]() ,b=
,b= ![]() 时,△QMN面积的最小值为
时,△QMN面积的最小值为 ![]() +
+ ![]() .
.
【解析】(Ⅰ)把M点坐标代入抛物线解析式可得到b与a的关系,可用a表示出抛物线解析式,化为顶点式可求得其顶点坐标;(Ⅱ)由直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,再判断其判别式大于0即可;(Ⅲ)(i)由(Ⅱ)的方程,可求得N点坐标,利用勾股定理可求得MN2 , 利用二次函数性质可求得MN长度的取值范围;(ii)设抛物线对称轴交直线与点E,则可求得E点坐标,利用S△QMN=S△QEN+S△QEM可用a表示出△QMN的面积,再整理成关于a的一元二次方程,利用判别式可得其面积的取值范围,可求得答案.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=2 ![]() ,则图中阴影部分的面积为 . (结果不取近似值)
,则图中阴影部分的面积为 . (结果不取近似值) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3 , 以OA3为直角边作第三个等腰直角三角形OA3A4 , …,依此规律,得到等腰直角三角形OA2017A2018 , 则点A2017的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AD于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计) 
(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥AB和引桥BC两部分组成(如图所示),建造前工程师用以下方式做了测量;无人机在A处正上方97m处的P点,测得B处的俯角为30°(当时C处被小山体阻挡无法观测),无人机飞行到B处正上方的D处时能看到C处,此时测得C处俯角为80°36′.
(长度均精确到1m,参考数据: ![]() ≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)
≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)
(1)求主桥AB的长度;
(2)若两观察点P、D的连线与水平方向的夹角为30°,求引桥BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com