
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 和过点
和过点![]() 的切线互相垂直,垂足为
的切线互相垂直,垂足为![]() ,直线
,直线![]() 、
、![]() 交于点
交于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
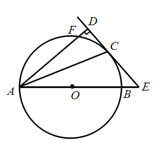
【答案】(1)见解析 (2)![]()
【解析】
(1)先通过切线的性质和垂直得出![]() ,然后有
,然后有![]() ,再根据等腰三角形的性质有
,再根据等腰三角形的性质有![]() ,通过等量代换即可得出
,通过等量代换即可得出![]() ,则结论可证;
,则结论可证;
(2)方法一:先利用圆周角定理和圆内接四边形的性质得出![]() ,然后利用
,然后利用![]() 得出
得出![]() ,则DF可求,进而AD可求,利用勾股定理可求出AC的长度,然后利用
,则DF可求,进而AD可求,利用勾股定理可求出AC的长度,然后利用![]() 得出
得出![]() ,进而求出AB的长度,最后利用平行线分线段成比例求解即可;
,进而求出AB的长度,最后利用平行线分线段成比例求解即可;
方法二:先利用圆周角定理和圆内接四边形的性质得出![]() ,然后利用
,然后利用![]() 得出
得出![]() ,则DF可求,进而AD可求,利用勾股定理可求出AC的长度,然后利用
,则DF可求,进而AD可求,利用勾股定理可求出AC的长度,然后利用![]() 得出
得出![]() ,进而求出AB的长度以及
,进而求出AB的长度以及![]() 然后利用
然后利用![]() 得
得![]() ,最后利用
,最后利用![]() 求解即可.
求解即可.
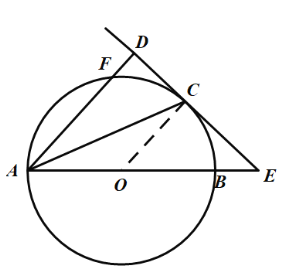
(1)证明:如图,连接![]() ,
,
![]() 和过点
和过点![]() 的切线互相垂直,垂足为
的切线互相垂直,垂足为![]() ,
,
![]()
![]() 是过点
是过点![]() 的切线,
的切线,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
即![]() 平分
平分![]() .
.
(2)方法一:
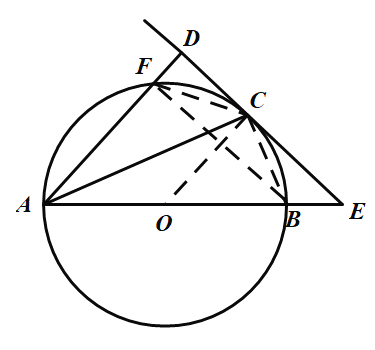
如图,连接![]() ,
,![]() ,
,![]() .
.
![]() 是
是![]() 的直径,
的直径,
![]() ,
,![]() .
.
![]() .
.
∵![]() ,
,
由(1)知![]() .
.
![]() .
.
![]() 四边形
四边形![]() 是圆内接四边形,
是圆内接四边形,
![]() ,
,
![]() ,
,
![]() .
.
由(1)知![]() ,
,
![]() .
.
![]() .
.
![]() .即
.即![]() .
.
解得![]() 或
或![]() (舍).
(舍).
![]() .
.
在![]() 中,
中,![]() .
.
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
![]() ,即
,即![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
![]() .
.
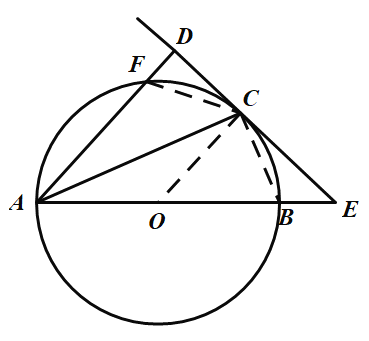
方法二:如图,连接![]() ,
,![]() .
.
![]() 是
是![]() 的直径,
的直径,
![]() ,
,![]() .
.
![]() .
.
∵![]() ,
,
由(1)知![]() .
.
![]() .
.
![]() 四边形
四边形![]() 是圆内接四边形,
是圆内接四边形,
![]() ,
,
![]() ,
,
![]() .
.
由(1)知![]() ,
,
![]() .
.
![]() .
.
![]() .即
.即![]() .
.
解得![]() 或
或![]() (舍).
(舍).
![]() .
.
在![]() 中,
中,![]() .
.
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
即![]() .
.
![]() .
.
∵![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() ,即
,即![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
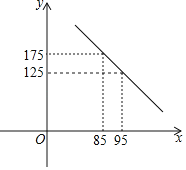
【题目】武汉“新冠肺炎”发生以来,某医疗公司积极复工,加班加点生产医用防护服,为防控一线助力.以下是该公司以往的市场调查,发现该公司防护服的日销售量y(套)与销售单价x(元)之间满足一次函数关系,如下图所示,关于日销售利润w(元)和销售单价x(元)的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 |
日销售利润w(元) | 875 | 1875 | 1875 |
(注:日销售利润=日销售量×(销售单价一成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围);
(2)根据函数图象和表格所提供的信息,填空:
该公司生产的防护服的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)该公司复工以后,在政府部门的帮助下,原材料采购成本比以往有了下降,平均起来,每生产一套防护服,成本比以前下降5元.该公司计划开展科技创新,以降低该产品的成本,如果在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
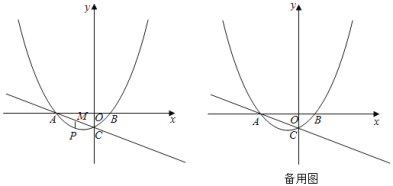
【题目】如图,抛物线![]() 交x轴于A,B两点,交y轴于点C.直线
交x轴于A,B两点,交y轴于点C.直线![]() 经过点A,C.
经过点A,C.
(1)求抛物线的解析式;
(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
①当![]() 是直角三角形时,求点P的坐标;
是直角三角形时,求点P的坐标;
②作点B关于点C的对称点![]() ,则平面内存在直线l,使点M,B,
,则平面内存在直线l,使点M,B,![]() 到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线
到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线![]() 的解析式.(k,b可用含m的式子表示)
的解析式.(k,b可用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
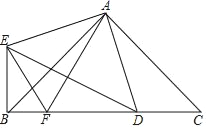
【题目】如图,△ABC和△ADE分别是以BC,DE为底边且顶角相等的等腰三角形,点D在线段BC上,AF平分DE交BC于点F,连接BE,EF.
(1)CD与BE相等?若相等,请证明;若不相等,请说明理由;
(2)若∠BAC=90°,求证:BF2+CD2=FD2.
查看答案和解析>>
科目:初中数学 来源: 题型:
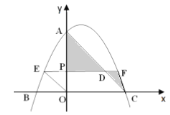
【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,点
两点,点![]() 是线段
是线段![]() 上的一个动点,过
上的一个动点,过![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).
(1)求抛物线的解析式.
(2)当四边形![]() 是平行四边形时,求点
是平行四边形时,求点![]() 的坐标.
的坐标.
(3)设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
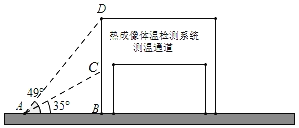
【题目】为保障师生复学复课安全,某校利用热成像体温检测系统,对入校师生进行体温检测.如图是测温通道示意图,在测温通道侧面A点测得∠DAB=49°,∠CAB=35°.若AB=3m,求显示牌的高度DC.(sin35°≈0.57,tan35°≈0.70,sin49°=0.75,tan49°≈1.15,结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
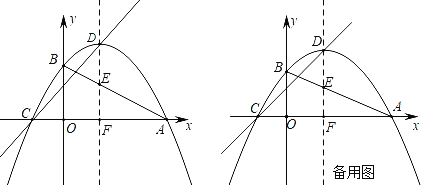
【题目】如图,抛物线y=ax2+x+c与x轴交于点A(6,0),C(﹣2,0),与y轴交于点B,抛物线的顶点为D,对称轴交AB于点E,交x轴于点F.
(1)求抛物线的解析式;
(2)P是抛物线上对称轴左侧一点,连接EP,若tan∠BEP=![]() ,求点P的坐标;
,求点P的坐标;
(3)M是直线CD上一点,N是抛物线上一点,试判断是否存在这样的点N,使得以点B,E,M,N为顶点的四边形是平行四边形,若存在,请直接写出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现
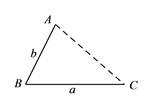
如图,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() .
.
填空:当点![]() 位于____________时,线段
位于____________时,线段![]() 的长取得最大值,且最大值为_________.(用含
的长取得最大值,且最大值为_________.(用含![]() ,
,![]() 的式子表示)
的式子表示)
(2)应用
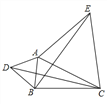
点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() .如图所示,分别以
.如图所示,分别以![]() ,
,![]() 为边,作等边三角形
为边,作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() ,
,![]() .
.
①找出图中与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②直接写出线段![]() 长的最大值.
长的最大值.
(3)拓展
如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 长的最大值及此时点
长的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O且AB=AC,延长BC至点D,使CD=CA,连接AD交⊙O于点E,连接BE、CE.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,EF=4,DE的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com