
【题目】如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4).
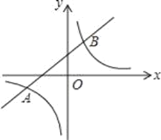
(1)求一次函数和反比例函数的表达式及点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数.
【答案】(1)y=x+2,![]() ,B(2,4);(2)-4<x<0或x>2
,B(2,4);(2)-4<x<0或x>2
【解析】
(1)设反比例函数的解析式为![]() (k≠0),把A点坐标代入即可得出k的值,进而得出反比例函数的解析式,再把B点坐标代入即可得出a的值,利用待定系数法即可得出一次函数的解析式;
(k≠0),把A点坐标代入即可得出k的值,进而得出反比例函数的解析式,再把B点坐标代入即可得出a的值,利用待定系数法即可得出一次函数的解析式;
(2)直接根据两函数的交点即可得出结论.
解:(1)设反比例函数![]() ,将A(﹣4,﹣2)代入
,将A(﹣4,﹣2)代入![]() 中得:k=8,
中得:k=8,
∴![]() ;
;
将B(a,4)代入![]() 中得:
中得:![]() ,
,
∴B(2,4);
设一次函数![]() ,将A(﹣4,﹣2),B(2,4)代入得:
,将A(﹣4,﹣2),B(2,4)代入得:
![]() ,
,
解得:![]() ,
,
∴一次函数解析式为:![]() ;
;
(2)根据题意,∵点A(﹣4,﹣2),B(2,4),
则由图像可知,
当![]() 时,x的取值范围是:
时,x的取值范围是:![]() 4<x<0或x>2;
4<x<0或x>2;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某家电生产厂家去年销往农村的某品牌洗碗机每台的售价![]() (元)与月份
(元)与月份![]() 之间满足函数关系
之间满足函数关系![]() ,去年的月销售量户(万台)与月份
,去年的月销售量户(万台)与月份![]() 之间成一次函数关系,其中两个月的销售情况如表:
之间成一次函数关系,其中两个月的销售情况如表:
月份: | 1月 | 5月 |
销售量: | 3.9万台 | 4.3万台 |
(1)求该品牌洗碗机在去年哪个月销往农村的销售金额最大?最大是多少?(提示:销售金额=销量×售价)
(2)经统计和计算.得到此洗碗机在农村地区的销售数据,如表:
销售数据信息表 | 售价(元/台) | 销量(万台) | 补贴金额(万元) |
去年12月份 | 2000 | 5 | / |
今年2月份 |
|
| / |
今年3月份 |
|
| 312 |
由于国家实施“家电下乡政策”,所以今年3月份国家按该产品售价的13%给子财政补贴,共补贴了312万元,从表格中,我们可以看出:今年3月份与今年2月份相比较,售价保持不变,但销量增加了1.5万台.今年2月份与去年12月份相比较,售价下降了![]() %,销量下降了1.5
%,销量下降了1.5![]() %;请用
%;请用![]() 表示表格中的
表示表格中的![]() ,
,![]() ,并根据已知条件求出
,并根据已知条件求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
问题情境:在一次综合实践活动课上,同学们以菱形为对象,研究菱形旋转中的问题:已知,在菱形![]() 中,
中, ![]() 为对角线,
为对角线, ![]() ,
,![]() ,将菱形
,将菱形![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() (单位
(单位![]() ),旋转后的菱形为
),旋转后的菱形为![]() ,在旋转探究活动中提出下列问题,请你帮他们解决.
,在旋转探究活动中提出下列问题,请你帮他们解决.
观察证明:
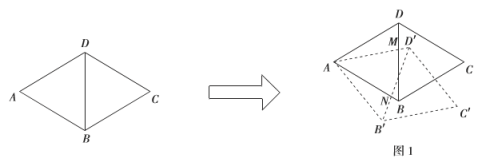
(1)如图1,若旋转角![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,请说明线段
,请说明线段![]() 与
与![]() 的数量关系;
的数量关系;
操作计算:
(2)如图2,连接![]() ,菱形
,菱形![]() 旋转的过程中,当
旋转的过程中,当![]() 与
与![]() 互相垂直时,
互相垂直时, ![]() 的长为 ;
的长为 ;
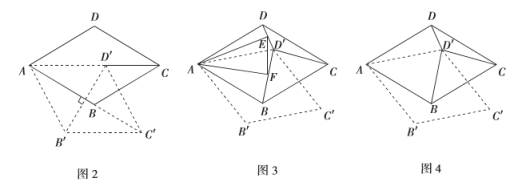
(3)如图3,若旋转角![]() ,分别连接
,分别连接![]() ,
,![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,连接
,连接![]() ,菱形
,菱形![]() 旋转的过程中,发现在
旋转的过程中,发现在![]() 中存在长度不变的线段
中存在长度不变的线段![]() ,请求出
,请求出![]() 长度;
长度;
操作探究:
(4)如图4,在(3)的条件下,请判断以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是什么特殊三角形,并说明理由.
三条线段长度为边的三角形是什么特殊三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
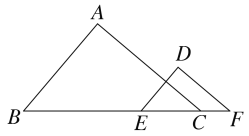
【题目】如图,已知点B、E、C、F在同一条直线上,∠A= ∠D,要使△ABC∽△DEF,还需添加一个条件,则添加的条件可以是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,(注:1尺=10寸)问这块圆柱形木材的直径是( )
寸,(注:1尺=10寸)问这块圆柱形木材的直径是( )
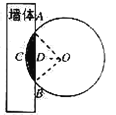
A.13寸B.6.5寸C.20寸D.26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
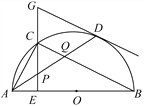
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的![]() ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?
(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com