
【题目】综合与实践:
问题情境:在一次综合实践活动课上,同学们以菱形为对象,研究菱形旋转中的问题:已知,在菱形![]() 中,
中, ![]() 为对角线,
为对角线, ![]() ,
,![]() ,将菱形
,将菱形![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() (单位
(单位![]() ),旋转后的菱形为
),旋转后的菱形为![]() ,在旋转探究活动中提出下列问题,请你帮他们解决.
,在旋转探究活动中提出下列问题,请你帮他们解决.
观察证明:
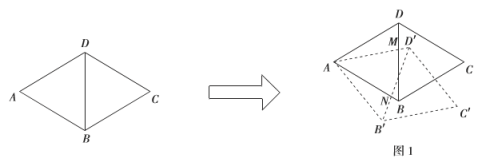
(1)如图1,若旋转角![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,请说明线段
,请说明线段![]() 与
与![]() 的数量关系;
的数量关系;
操作计算:
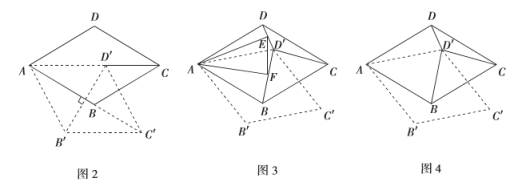
(2)如图2,连接![]() ,菱形
,菱形![]() 旋转的过程中,当
旋转的过程中,当![]() 与
与![]() 互相垂直时,
互相垂直时, ![]() 的长为 ;
的长为 ;
(3)如图3,若旋转角![]() ,分别连接
,分别连接![]() ,
,![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,连接
,连接![]() ,菱形
,菱形![]() 旋转的过程中,发现在
旋转的过程中,发现在![]() 中存在长度不变的线段
中存在长度不变的线段![]() ,请求出
,请求出![]() 长度;
长度;
操作探究:
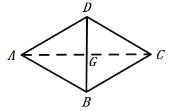
(4)如图4,在(3)的条件下,请判断以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是什么特殊三角形,并说明理由.
三条线段长度为边的三角形是什么特殊三角形,并说明理由.
【答案】(1)![]() ,理由详见解析;(2)
,理由详见解析;(2)![]() ;(3)2;(4)以
;(3)2;(4)以![]() ,
,![]() ,
,![]() 三条线段为边的三角形是直角三角形,理由详见解析.
三条线段为边的三角形是直角三角形,理由详见解析.
【解析】
(1)根据菱形的性质以及旋转的性质,证得![]() ,根(
,根(![]() 证得
证得![]() ≌
≌![]() ,可以得到结论;
,可以得到结论;
(2)根据菱形的性质以及条件![]() 与
与![]() 互相垂直,证明
互相垂直,证明![]() 、
、![]() 在同一直线上,利用锐角三角函数求得对角线的长,继而求得结论;
在同一直线上,利用锐角三角函数求得对角线的长,继而求得结论;
(3)利用等腰三角形三线合一的性质,![]() 是
是![]() 的中位线,从而证明
的中位线,从而证明![]() ;
;
(4) 以![]() 为边向外作等边三角形,利用等边三角形的性质以及
为边向外作等边三角形,利用等边三角形的性质以及![]() 证得
证得![]() ≌
≌![]() ,得到
,得到![]() ,把
,把![]() ,
,![]() ,
,![]() 三条线段归结到一个三角形中,易证得
三条线段归结到一个三角形中,易证得![]() 是直角三角形,从而得到结论.
是直角三角形,从而得到结论.
(1) ![]() ,理由如下:
,理由如下:
∵四边形![]() 是菱形
是菱形
∴![]()
∴![]()
由旋转的性质可得: ![]() ,
,![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
即![]()
在![]() 和
和![]() 中
中
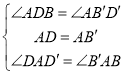
∴![]() ≌
≌![]() (
(![]() )
)
∴![]()
(2) 菱形![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() 平分
平分![]() (等腰三角形三线合一),
(等腰三角形三线合一),
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() 、
、![]() 在同一直线上,
在同一直线上,
如图,菱形![]() 中,
中, ![]() 为对角线,
为对角线, ![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
故答案是:![]()
(3)如图,连接![]() ,由题可得:
,由题可得: ![]()
∵![]()
∴![]() (等腰三角形三线合一),同理
(等腰三角形三线合一),同理![]()
∴![]() 是
是![]() 的中位线
的中位线
∴![]()
∵四边形![]() 是菱形
是菱形
∴![]()
又∵![]() ,
,![]() 是等边三角形
是等边三角形
∴![]()
∴![]()
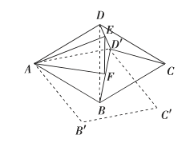
(4)以![]() ,
,![]() ,
,![]() 三条线段为边的三角形是直角三角形,理由如下:
三条线段为边的三角形是直角三角形,理由如下:
如图,以![]() 为边向外作等边三角形
为边向外作等边三角形![]() ,连接
,连接![]() ,
,![]()
∵四边形![]() 是菱形,
是菱形, ![]()
∴![]() 与
与![]() 是等边三角形,
是等边三角形, ![]()
由(3)可知: ![]() 与
与![]() 都是等腰三角形
都是等腰三角形
∴![]()
![]()
∵![]() 与
与![]() 是等边三角形
是等边三角形
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中

∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,
,![]()
∴![]()
∴![]() 是直角三角形
是直角三角形
即以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是直角三角形.
三条线段长度为边的三角形是直角三角形.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如下表格:
的图象可以得到如下表格:
|
|
|
|
|
|
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可得到如下表格:
的图象可得到如下表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() 的图象;
的图象;
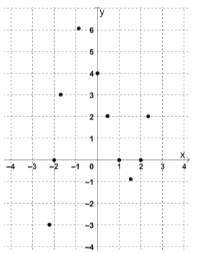
观察函数![]() 的图象,
的图象,
补全下面的表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法,解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=x+m的图象与x轴y轴分别交于点A、B,与反比例函数y2=![]() (x<0)的图象分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)的图象分别交于点C、D,且C点的坐标为(﹣1,2).
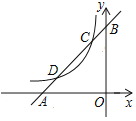
(1)分别求出一次函数及反比例函数的关系式;
(2)求出点D的坐标并直接写出y1>y2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
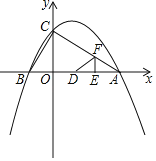
【题目】综合与探究:
已知二次函数y=﹣![]() x2+
x2+![]() x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求证:△ABC为直角三角形;
(3)如图,动点E,F同时从点A出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() (每个方格的边长均为1个单位长度).
(每个方格的边长均为1个单位长度).
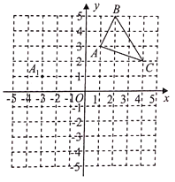
(1)将![]() 平移,使点
平移,使点![]() 移动到点
移动到点![]() ,请画出
,请画出![]() ;
;
(2)作出![]() 关于
关于![]() 点成中心对称的
点成中心对称的![]() ,并直接写出
,并直接写出![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)![]() 与
与![]() 是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.
是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.
(1)求证:CP为⊙O的切线;
(2)若BP=1,CP=![]() ,求 ⊙O的半径;
,求 ⊙O的半径;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4).
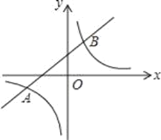
(1)求一次函数和反比例函数的表达式及点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com