
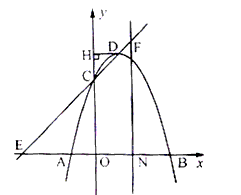
�⣺��1����y=0�ã�ax2-2ax-3a=0��
��a��0��
��x2-2x-3=0��
���x1=-1��x2=3��
���A�����꣨-1��0������B�����꣨3��0����
��2����y=ax2-2ax-3a��
��x=0����y=-3a��
��C��0��-3a����
�֡�y=ax2-2ax-3a=a��x-1��2-4a��
��D��1��-4a����
��DH=1��CH=-4a-��-3a��=-a��
��-a=1��
��a=-1��
��C��0��3����D��1��4����
��ֱ��CD�Ľ���ʽΪy=kx+b��
��C��D������������ã�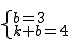 ��
��
���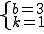 ��
��
��ֱ��CD�Ľ���ʽΪy=x+3��
��3�����ڣ��ɣ�2���ã�E��-3��0����N��-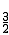 ��0����
��0����
��F��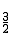 ��
��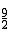 ����EN=
����EN=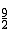 ��
��
��MQ��CD��Q��
��������������ĵ�M��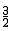 ��m����
��m����
��FM=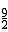 -m��
-m��
EF=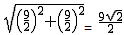 ��
��
MQ=OM=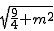 ��
��
������ã�Rt��FQM��Rt��FNE��
��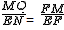 ��
��
������4m2+36m-63=0��
��m2+9m=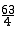 ��
��
m2+9m+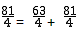
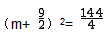
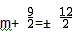
��m1=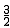 ��m2=-
��m2=-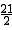 ��
��
���M������ΪM1��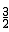 ��
��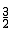 ����M2��
����M2��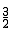 ��-
��-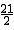 ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��x�����һ������ΪE��
��x�����һ������ΪE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪������y=ax2+bx+c������b��0��c��0���Ķ���P��x���ϣ���y�ύ�ڵ�Q��������ԭ��O����OA��PQ������ΪA����OA=
��ͼ����֪������y=ax2+bx+c������b��0��c��0���Ķ���P��x���ϣ���y�ύ�ڵ�Q��������ԭ��O����OA��PQ������ΪA����OA=| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| c | a |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com