
°ĺŐ‚ńŅ°ŅÕľĘŔ «ł ňŗ °≤©őÔĻ›Ķń’ÚĻ›÷ģĪ¶°™°™Õ≠Īľ¬Ū£¨”÷≥∆°į¬ŪŐ§∑…—ŗ°Ī£¨”ŕ1969ńÍ10‘¬≥ŲÕŃ”ŕőšÕĢ –Ķńņ◊Ő®ļļńĻ£¨1983ńÍ10‘¬ĪĽĻķľ“¬√”őĺ÷»∑∂®ő™÷–Ļķ¬√”őĪÍ÷ĺ£¨‘ŕļ‹∂ŗ¬√”ő≥« –ĶńĻ„≥°…Ō∂ľ”–°į¬ŪŐ§∑…—ŗ°ĪĶŮň‹£¨ń≥—ßŌį–°◊ťį—≤‚ŃŅĪĺ≥« –Ļ„≥°Ķń°į¬ŪŐ§∑…—ŗ°ĪĶŮň‹£®ÕľĘŕ£©◊ÓłŖĶ„ņŽĶō√śĶńłŖ∂»◊ųő™“ĽīőŅőŐ‚ĽÓ∂Į£¨Õ¨—ß√«÷∆∂®Ńň≤‚ŃŅ∑Ĺįł£¨≤ĘÕÍ≥…Ńň ĶĶō≤‚ŃŅ£¨≤‚Ķ√ĹŠĻŻ»ÁŌ¬ĪŪ£ļ
ŅőŐ‚ | ≤‚ŃŅ°į¬ŪŐ§∑…—ŗ°ĪĶŮň‹◊ÓłŖĶ„ņŽĶō√śĶńłŖ∂» | |||
≤‚ŃŅ ĺ“‚Õľ |
| »ÁÕľ£¨ĶŮň‹Ķń◊ÓłŖĶ„ | ||
≤‚ŃŅ żĺ› |
|
|
| “«∆ų |
|
| 5√◊ |
| |
«Žń„łýĺ›…ŌĪŪ÷–Ķń≤‚ŃŅ żĺ›£¨įÔ÷ķł√–°◊ť«ů≥Ų°į¬ŪŐ§∑…—ŗ°ĪĶŮň‹◊ÓłŖĶ„ņŽĶō√śĶńłŖ∂»£®ĹŠĻŻĪ£ŃŰ“ĽőĽ–° ż£©£ģ£®≤őŅľ żĺ›£ļ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £©
£©


| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ√ŅłŲĪŖ≥§∂ľő™![]() Ķń–°’ż∑Ĺ–ő◊ť≥…ĶńÕÝłŮ÷–£¨–°’ż∑Ĺ–őĶń∂•Ķ„Ĺ–◊ŲłŮĶ„£ģŌŖ∂ő
Ķń–°’ż∑Ĺ–ő◊ť≥…ĶńÕÝłŮ÷–£¨–°’ż∑Ĺ–őĶń∂•Ķ„Ĺ–◊ŲłŮĶ„£ģŌŖ∂ő![]() Ķń∂ňĶ„
Ķń∂ňĶ„![]() ĺý‘ŕłŮĶ„…Ō£ģ
ĺý‘ŕłŮĶ„…Ō£ģ
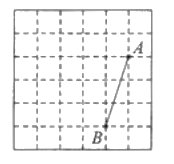
£®1£©ŌŖ∂ő![]() Ķń≥§∂»Ķ»”ŕ £Ľ
Ķń≥§∂»Ķ»”ŕ £Ľ
£®2£©ĹęŌŖ∂ő![]() »∆Ķ„
»∆Ķ„![]() ńś Ī’Ž–ż◊™
ńś Ī’Ž–ż◊™![]() Ķ√ĶĹ
Ķ√ĶĹ![]() £¨‘ŕÕľ÷–Ľ≠≥Ų
£¨‘ŕÕľ÷–Ľ≠≥Ų![]() £¨≤ĘѨŊ
£¨≤ĘѨŊ![]() £ģ
£ģ
£®3£©‘ŕŌŖ∂ő![]() …Ō»∑∂®“ĽĶ„
…Ō»∑∂®“ĽĶ„![]() ѨŊ
ѨŊ![]() £¨ ĻĶ√
£¨ ĻĶ√![]() ”Ž
”Ž![]() Ķń√śĽżĪ»ő™
Ķń√śĽżĪ»ő™![]() £ģ
£ģ
ňĶ√ų£ļ“‘…Ō◊ųÕľ÷Ľ”√őřŅŐ∂»Ķń÷Ī≥ŖĽ≠Õľ£¨Ī£ŃŰĽ≠ÕľļŘľ££¨≤Ľ–īĽ≠∑®£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“ĽīőļĮ ż![]() ĶńÕľŌů”Ž∑īĪ»ņżļĮ ż
ĶńÕľŌů”Ž∑īĪ»ņżļĮ ż![]() ĶńÕľŌůŌŗĹĽ£¨∆š÷–“ĽłŲĹĽĶ„ĶńļŠ◊ÝĪÍ «2£ģ
ĶńÕľŌůŌŗĹĽ£¨∆š÷–“ĽłŲĹĽĶ„ĶńļŠ◊ÝĪÍ «2£ģ
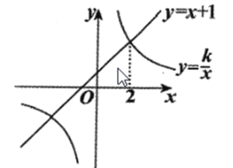
£®1£©«ů∑īĪ»ņżļĮ żĶńĪŪīÔ Ĺ£Ľ
£®2£©Ĺę“ĽīőļĮ ż![]() ĶńÕľŌůŌÚŌ¬∆Ĺ“∆2łŲĶ•őĽ£¨«ů∆Ĺ“∆ļůĶńÕľŌů”Ž∑īĪ»ņżļĮ ż
ĶńÕľŌůŌÚŌ¬∆Ĺ“∆2łŲĶ•őĽ£¨«ů∆Ĺ“∆ļůĶńÕľŌů”Ž∑īĪ»ņżļĮ ż![]() ÕľŌůĶńĹĽĶ„◊ÝĪÍ£Ľ
ÕľŌůĶńĹĽĶ„◊ÝĪÍ£Ľ
£®3£©÷ĪĹ”–ī≥Ų“ĽłŲ“ĽīőļĮ ż£¨ Ļ∆šĻżĶ„![]() £¨«“”Ž∑īĪ»ņżļĮ ż
£¨«“”Ž∑īĪ»ņżļĮ ż![]() ĶńÕľŌů√Ľ”–ĻęĻ≤Ķ„£ģ
ĶńÕľŌů√Ľ”–ĻęĻ≤Ķ„£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
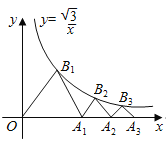
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨![]() £¨
£¨![]() £¨
£¨![]() £¨°≠£¨
£¨°≠£¨![]() £¨∂ľ «“ĽĪŖ‘ŕ
£¨∂ľ «“ĽĪŖ‘ŕ![]() ÷Š…ŌĶńĶ»ĪŖ»żĹ«–ő£¨Ķ„
÷Š…ŌĶńĶ»ĪŖ»żĹ«–ő£¨Ķ„![]() £¨
£¨![]() £¨
£¨![]() £¨°≠£¨
£¨°≠£¨![]() ∂ľ‘ŕ∑īĪ»ņżļĮ ż
∂ľ‘ŕ∑īĪ»ņżļĮ ż![]() ĶńÕľŌů…Ō£¨Ķ„
ĶńÕľŌů…Ō£¨Ķ„![]() £¨
£¨![]() £¨
£¨![]() £¨°≠£¨
£¨°≠£¨![]() £¨∂ľ‘ŕ
£¨∂ľ‘ŕ![]() ÷Š…Ō£¨‘Ú
÷Š…Ō£¨‘Ú![]() Ķń◊ÝĪÍő™________£ģ
Ķń◊ÝĪÍő™________£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
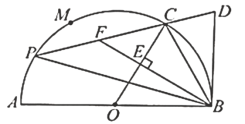
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨![]() ő™įŽ°—OĶń÷Īĺ∂£¨
ő™įŽ°—OĶń÷Īĺ∂£¨![]() £¨
£¨![]() «įŽ‘≤…ŌĶń»żĶ»∑÷Ķ„£¨
«įŽ‘≤…ŌĶń»żĶ»∑÷Ķ„£¨![]() £¨
£¨![]() ”ŽįŽ°—OŌŗ«–”ŕĶ„
”ŽįŽ°—OŌŗ«–”ŕĶ„![]() £¨Ķ„
£¨Ķ„![]() ő™
ő™![]() …Ō“Ľ∂ĮĶ„£®≤Ľ”ŽĶ„
…Ō“Ľ∂ĮĶ„£®≤Ľ”ŽĶ„![]() £¨
£¨![]() ÷ōļŌ£©£¨÷ĪŌŖ
÷ōļŌ£©£¨÷ĪŌŖ![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨
£¨![]() ”ŕĶ„
”ŕĶ„![]() £¨—”≥§
£¨—”≥§![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨‘ÚŌ¬Ń–ĹŠ¬Ř’ż»∑Ķń «______________£ģ£®–ī≥Ųňý”–’ż»∑ĹŠ¬ŘĶń–ÚļŇ£©
£¨‘ÚŌ¬Ń–ĹŠ¬Ř’ż»∑Ķń «______________£ģ£®–ī≥Ųňý”–’ż»∑ĹŠ¬ŘĶń–ÚļŇ£©
ĘŔ![]() £ĽĘŕ
£ĽĘŕ![]() Ķń≥§ő™
Ķń≥§ő™![]() £ĽĘŘ
£ĽĘŘ![]() £ĽĘ‹
£ĽĘ‹![]() £ĽĘ›
£ĽĘ›![]() ő™∂®÷Ķ£ģ
ő™∂®÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
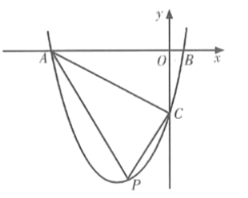
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨Ň◊őÔŌŖ![]() ĹĽ
ĹĽ![]() ÷Š”ŕ
÷Š”ŕ![]() £¨
£¨![]() ŃĹĶ„£¨ĹĽ
ŃĹĶ„£¨ĹĽ![]() ÷Š”ŕĶ„
÷Š”ŕĶ„![]() £¨«“
£¨«“![]() £¨Ķ„
£¨Ķ„![]() «Ķ໿ŌůŌřńŕŇ◊őÔŌŖ…ŌĶń“Ľ∂ĮĶ„£ģ
«Ķ໿ŌůŌřńŕŇ◊őÔŌŖ…ŌĶń“Ľ∂ĮĶ„£ģ
£®1£©«ůīňŇ◊őÔŌŖĶńĪŪīÔ Ĺ£Ľ
£®2£©»Ű![]() £¨«ůĶ„
£¨«ůĶ„![]() Ķń◊ÝĪÍ£Ľ
Ķń◊ÝĪÍ£Ľ
£®3£©Ń¨Ĺ”![]() £¨«ů
£¨«ů![]() √śĽżĶń◊Óīů÷Ķľįīň ĪĶ„
√śĽżĶń◊Óīů÷Ķľįīň ĪĶ„![]() Ķń◊ÝĪÍ£ģ
Ķń◊ÝĪÍ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁĪŪ «“ĽłŲ4°Ń4£®4––4Ń–Ļ≤16łŲ°į ż°Ī◊ť≥…£©Ķń∆ś√Ó∑Ĺ’ů£¨ī”’‚łŲ∑Ĺ’ů÷–—°ňńłŲ°į ż°Ī£¨∂Ý«“’‚ňńłŲ°į ż°Ī÷–Ķń»őļőŃĹłŲ≤Ľ‘ŕÕ¨“Ľ––£¨“≤≤Ľ‘ŕÕ¨“ĽŃ–£¨”–ļ‹∂ŗ—°∑®£¨į—√Ņīő—°≥ŲĶńňńłŲ°į ż°ĪŌŗľ”£¨∆šļÕ «∂®÷Ķ£¨‘Ú∑Ĺ’ů÷–Ķ໿––»żŃ–Ķń°į ż°Ī «£®°°°°£©
30 |
| 2 | 22 |
©Ā3 | ©Ā2 | ©Ā | 0 |
|©Ā5| | 6 | 23 | |
£® | 4 |
| £® |
A. 5 B. 6 C. 7 D. 8
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
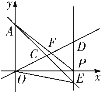
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨“ĽīőļĮ ż![]() ĶńÕľŌů”Ž
ĶńÕľŌů”Ž![]() ÷ŠĹĽ”ŕĶ„
÷ŠĹĽ”ŕĶ„![]() £¨”Ž’żĪ»ņżļĮ ż
£¨”Ž’żĪ»ņżļĮ ż![]() ĶńÕľŌůĹĽ”ŕĶ„
ĶńÕľŌůĹĽ”ŕĶ„![]() £¨Ķ„
£¨Ķ„![]() ‘ŕ
‘ŕ![]() ÷ŠĶń’żįŽ÷Š…Ō£¨«“Ķ„
÷ŠĶń’żįŽ÷Š…Ō£¨«“Ķ„![]() ĶńļŠ◊ÝĪÍő™
ĶńļŠ◊ÝĪÍő™![]() £¨ĻżĶ„
£¨ĻżĶ„![]() ◊ų
◊ų![]() ÷ŠĶńīĻŌŖ£¨∑÷ĪūĹĽ“ĽīőļĮ ż
÷ŠĶńīĻŌŖ£¨∑÷ĪūĹĽ“ĽīőļĮ ż![]() ĶńÕľŌů”ŕĶ„
ĶńÕľŌů”ŕĶ„![]() £¨ĹĽ’żĪ»ņżļĮ ż
£¨ĹĽ’żĪ»ņżļĮ ż![]() ĶńÕľŌů”ŕĶ„
ĶńÕľŌů”ŕĶ„![]() £ģ
£ģ
£®1£©«ůĶ„![]() Ķń◊ÝĪÍ£Ľ
Ķń◊ÝĪÍ£Ľ
£®2£©ĶĪ![]() ő™ļő÷Ķ Ī£¨
ő™ļő÷Ķ Ī£¨![]() £Ľ
£Ľ
£®3£©Ń¨Ĺ”![]() °Ę
°Ę![]() £¨
£¨![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨“—÷™
£¨“—÷™![]() £¨‘ŕŐ÷¬Ř
£¨‘ŕŐ÷¬Ř![]() Ķń√śĽż”Ž
Ķń√śĽż”Ž![]() √śĽżĶńīů–°ő Ő‚ Ī£¨ľőľő»Ōő™
√śĽżĶńīů–°ő Ő‚ Ī£¨ľőľő»Ōő™![]() £¨šŅšŅ»Ōő™
£¨šŅšŅ»Ōő™![]() £¨«Žń„◊ųő™–°∑®ĻŔ£¨įÔ÷ķňŻ√«ŃĹ»ň∆ņŇ–£¨ň≠ĶńňĶ∑®’ż»∑£ģ
£¨«Žń„◊ųő™–°∑®ĻŔ£¨įÔ÷ķňŻ√«ŃĹ»ň∆ņŇ–£¨ň≠ĶńňĶ∑®’ż»∑£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
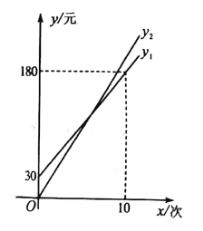
°ĺŐ‚ńŅ°Ņ Ó∆ŕĹę÷Ń£¨ń≥Ĺ°…Ūĺ„ņ÷≤Ņ√śŌÚ—ß…ķÕ∆≥Ų Ó∆ŕ”ŇĽ›ĽÓ∂Į£¨ĽÓ∂Į∑Ĺįł»ÁŌ¬£ģ
∑Ĺįł“Ľ£ļĻļ¬Ú“Ľ’Ň—ß…ķ Ó∆ŕ◊®ŌŪŅ®£¨√ŅīőĹ°…Ū∑—”√įīŃý’ؔҼ›£Ľ
∑Ĺįł∂Ģ£ļ≤ĽĻļ¬Ú—ß…ķ Ó∆ŕ◊®ŌŪŅ®£¨√ŅīőĹ°…Ū∑—”√įīįň’ؔҼ›£Ľ
…Ťń≥—ß…ķ Ó∆ŕĹ°…Ū![]() (īő)£¨įī’’∑Ĺįł“Ľňý–Ť∑—”√ő™
(īő)£¨įī’’∑Ĺįł“Ľňý–Ť∑—”√ő™![]() £¨(‘™)£¨«“
£¨(‘™)£¨«“![]() £Ľįī’’∑Ĺįł∂Ģňý–Ť∑—”√ő™
£Ľįī’’∑Ĺįł∂Ģňý–Ť∑—”√ő™![]() (‘™) £¨«“
(‘™) £¨«“![]() ∆šļĮ żÕľŌů»ÁÕľňý ĺ£ģ
∆šļĮ żÕľŌů»ÁÕľňý ĺ£ģ
![]() «ů
«ů![]() ļÕ
ļÕ![]() Ķń÷Ķ£¨≤ĘňĶ√ųňŁ√«Ķń Ķľ “‚“Ś£Ľ
Ķń÷Ķ£¨≤ĘňĶ√ųňŁ√«Ķń Ķľ “‚“Ś£Ľ
![]() «ůīÚ’Ř«įĶń√ŅīőĹ°…Ū∑—”√ļÕ
«ůīÚ’Ř«įĶń√ŅīőĹ°…Ū∑—”√ļÕ![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
![]() įňńÍľ∂—ß…ķ–°Ľ™ľ∆Ľģ Ó∆ŕ«įÕýł√ĺ„ņ÷≤ŅĹ°…Ū
įňńÍľ∂—ß…ķ–°Ľ™ľ∆Ľģ Ó∆ŕ«įÕýł√ĺ„ņ÷≤ŅĹ°…Ū![]() īő£¨”¶—°‘Ůńń÷÷∑Ĺįłňý–Ť∑—”√łŁ…Ŕ?ňĶ√ųņŪ”…£ģ
īő£¨”¶—°‘Ůńń÷÷∑Ĺįłňý–Ť∑—”√łŁ…Ŕ?ňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com