
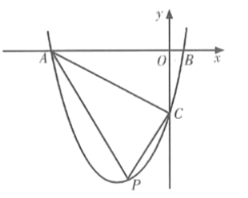
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,且
,且![]() ,点
,点![]() 是第三象限内抛物线上的一动点.
是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)连接![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)(
;(2)(![]() ,
,![]() );(3)
);(3)![]() 面积的最大值是8;点
面积的最大值是8;点![]() 的坐标为(
的坐标为(![]() ,
,![]() ).
).
【解析】
(1)由二次函数的性质,求出点C的坐标,然后得到点A、点B的坐标,再求出解析式即可;
(2)由![]() ,则点P的纵坐标为
,则点P的纵坐标为![]() ,代入解析式,即可求出点P的坐标;
,代入解析式,即可求出点P的坐标;
(3)先求出直线AC的解析式,过点P作PD∥y轴,交AC于点D,则![]() ,设点P为(
,设点P为(![]() ,
,![]() ),则点D为(
),则点D为(![]() ,
,![]() ),求出PD的长度,利用二次函数的性质,即可得到面积的最大值,再求出点P的坐标即可.
),求出PD的长度,利用二次函数的性质,即可得到面积的最大值,再求出点P的坐标即可.
解:(1)在抛物线![]() 中,
中,
令![]() ,则
,则![]() ,
,
∴点C的坐标为(0,![]() ),
),
∴OC=2,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴点A为(![]() ,0),点B为(
,0),点B为(![]() ,0),
,0),
则把点A、B代入解析式,得
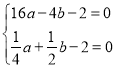 ,解得:
,解得:![]() ,
,
∴![]() ;
;
(2)由题意,∵![]() ,点C为(0,
,点C为(0,![]() ),
),
∴点P的纵坐标为![]() ,
,
令![]() ,则
,则![]() ,
,
解得:![]() ,
,![]() ,
,
∴点P的坐标为(![]() ,
,![]() );
);
(3)设直线AC的解析式为![]() ,则
,则
把点A、C代入,得
![]() ,解得:
,解得: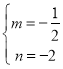 ,
,
∴直线AC的解析式为![]() ;
;
过点P作PD∥y轴,交AC于点D,如图:
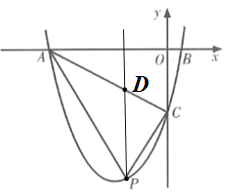
设点P 为(![]() ,
,![]() ),则点D为(
),则点D为(![]() ,
,![]() ),
),
∴![]() ,
,
∵OA=4,
∴![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 取最大值8;
取最大值8;
∴![]() ,
,
∴点P的坐标为(![]() ,
,![]() ).
).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知:函数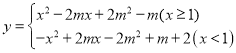 .
.
(1)当![]() 时,
时,
①求![]() 随
随![]() 增大而增大时,
增大而增大时,![]() 的取值范围;
的取值范围;
②当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
③当![]() 时,设
时,设![]() 的最大值与最小值之差为
的最大值与最小值之差为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() ,连结
,连结![]() .当此函数的图象与线段
.当此函数的图象与线段![]() 只有两个公共点时,直接写出
只有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 为对角线
为对角线![]() 的中点.
的中点.
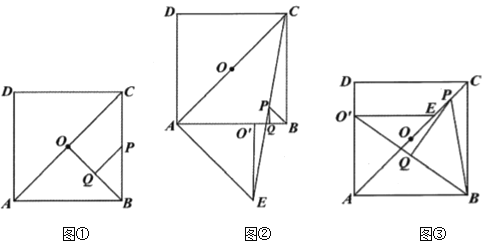
(1)问题解决:如图①,连接![]() ,分别取
,分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连接
,连接![]() ,则
,则![]() 与
与![]() 的数量关系是_____,位置关系是____;
的数量关系是_____,位置关系是____;
(2)问题探究:如图②,![]() 是将图①中的
是将图①中的![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到的三角形,连接
得到的三角形,连接![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() .判断
.判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(3)拓展延伸:如图③,![]() 是将图①中的
是将图①中的![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到的三角形,连接
得到的三角形,连接![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() .若正方形
.若正方形![]() 的边长为1,求
的边长为1,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线![]() 与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
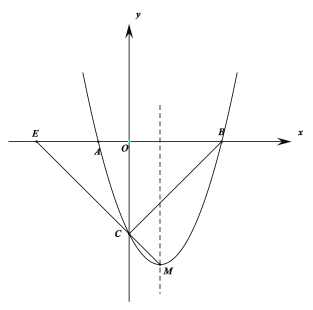
(1)求点C及顶点M的坐标.
(2)若点N是第四象限内抛物线上的一个动点,连接![]() 求
求![]() 面积的最大值及此时点N的坐标.
面积的最大值及此时点N的坐标.
(3)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.
(4)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P、E、O为顶点的三角形与![]() 相似.若存在,求出点P的坐标;若不存在,请说明理由.
相似.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
课题 | 测量“马踏飞燕”雕塑最高点离地面的高度 | |||
测量示意图 |
| 如图,雕塑的最高点 | ||
测量数据 |
|
|
| 仪器 |
|
| 5米 |
| |
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,关于
中,关于![]() 的二次函数
的二次函数![]() 的图象过点
的图象过点![]() ,
,![]() .
.
(1)求这个二次函数的表达式;
(2)求当![]() 时,
时,![]() 的最大值与最小值的差;
的最大值与最小值的差;
(3)一次函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象交点的横坐标分别是
的图象交点的横坐标分别是![]() 和
和![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:

(1)这次抽样调查中,共调查了 名学生;
(2)补全两幅统计图;
(3)根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是该直线上不同于
是该直线上不同于![]() 的点,且
的点,且![]() .
.
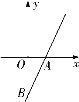
(1)写出![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)过动点![]() 且垂直于
且垂直于![]() 轴的直线与直线
轴的直线与直线![]() 交于点
交于点![]() ,若点
,若点![]() 不在线段
不在线段![]() 上,求
上,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 与直线
与直线![]() 所夹锐角为
所夹锐角为![]() ,请直接写出直线
,请直接写出直线![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com