
【题目】已知二次函数![]() .
.
(Ⅰ)已知![]() ,若二次函数图象与
,若二次函数图象与![]() 轴有唯一公共点,求
轴有唯一公共点,求![]() 的值;
的值;
(Ⅱ)已知![]() .
.
(ⅰ)当![]() 时,二次函数图象与
时,二次函数图象与![]() 轴有且只有一个公共点,求
轴有且只有一个公共点,求![]() 的取值范围;
的取值范围;
(ⅱ)当![]() 时,
时,![]() 有最小值
有最小值![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)(ⅰ)b的取值范围
;(Ⅱ)(ⅰ)b的取值范围![]() <b≤
<b≤![]() 或1≤b<3;(ⅱ)b的值为
或1≤b<3;(ⅱ)b的值为![]() 或
或![]() .
.
【解析】
(Ⅰ)先根据![]() 化简二次函数的解析式,再根据判别式△=
化简二次函数的解析式,再根据判别式△=![]() 即可得出b的值
即可得出b的值
(Ⅱ)(ⅰ)先根据已知条件得出方程的两个根![]() ,
,![]() ,再由
,再由![]() 即可得出b的取值范围;
即可得出b的取值范围;
(ⅱ)先根据已知条件得出抛物线的解析式![]() 和对称轴x=
和对称轴x=![]() ,再根据对称轴和
,再根据对称轴和![]() 、以及y的最小值分三种情况进行讨论即可
、以及y的最小值分三种情况进行讨论即可
(Ⅰ)当a=c=1,抛物线![]() ;且与x轴有唯一公共点.
;且与x轴有唯一公共点.
对于方程![]() ,判别式△=
,判别式△=![]() ,有
,有![]() .
.
(Ⅱ)(ⅰ)当![]() 时,∵
时,∵![]() ;
;
∴![]() ,
,![]() ;
;
当![]() <
<![]() <1时,
<1时,![]() <
<![]() ≤1,解得
≤1,解得![]() ≤b<3;
≤b<3;
当![]() <
<![]() <1时,
<1时,![]() ≤
≤![]() <1,解得
<1,解得![]() <b≤1;
<b≤1;
∵抛物线与x轴有且只有一个公共点,
∴b的取值范围![]() <b≤
<b≤![]() 或1≤b<3;
或1≤b<3;
(ⅱ)当![]() 时,
时,![]() ,抛物线
,抛物线![]() ;
;
图象开口向上,对称轴为直线x=![]() ,
,
①当b≤![]() ≤b+3时,即﹣2≤b≤0,∴当x=
≤b+3时,即﹣2≤b≤0,∴当x=![]() 时,
时,![]() ;
;
②当![]() <b,即b>0时,在自变量x的值满足b≤x≤b+3的情况下,y随x的增大而增大,
<b,即b>0时,在自变量x的值满足b≤x≤b+3的情况下,y随x的增大而增大,
∴当x=b时,![]() 为最小值,
为最小值,
∴![]() ,解得,
,解得,![]() <0(舍去),
<0(舍去),![]() ;
;
③当![]() >b+3,即b<﹣2,在自变量x的值满足b≤x≤+3的情况下,y随x的增大而减小,
>b+3,即b<﹣2,在自变量x的值满足b≤x≤+3的情况下,y随x的增大而减小,
∴当x=b+3时,![]() 为最小值,
为最小值,
∴![]() .解得,
.解得,![]() >﹣2(舍去),
>﹣2(舍去),![]() ;
;
综上所述:b的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:点E是正方形ABCD中边AB的中点.
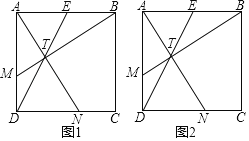
(1)如图1,点T为线段DE上一点,连接BT并延长交AD于点M,连接AT并延长交CD于点N,且AM=DN.试判断线段AN与线段BM的关系,并证明;求证:点M是线段AD的黄金分割点.
(2)如图2,在AD边上取一点M,满足AM2=DMDA时,连接BM交DE于点T,连接AT并延长交DC于点N,求tan∠MTD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋中有大小形状和质地等完全相同的![]() 个小球,它们分别标有数字
个小球,它们分别标有数字![]() ,从袋中任意摸出一小球(不放回),将袋中的小球搅匀后,再从袋中摸出另一小球.
,从袋中任意摸出一小球(不放回),将袋中的小球搅匀后,再从袋中摸出另一小球.
(1)请你用列表或画树状图的方法表示摸出小球上的数字可能出现的所有结果;
(2)规定:如果摸出的两个小球上的数字都是方程![]() 的根,则小明贏;如果摸出的两个小球上的数字都不是方程
的根,则小明贏;如果摸出的两个小球上的数字都不是方程![]() 的根,则小亮赢.你认为这个游戏规则对小明、小亮双方公平吗?请说明理由.
的根,则小亮赢.你认为这个游戏规则对小明、小亮双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴分别交于
与坐标轴分别交于![]() ,
,![]() ,
,![]() 三点,连接
三点,连接![]() ,
,![]() .
.
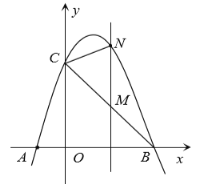
(1)直接写出![]() ,
,![]() ,
,![]() 三点的坐标;
三点的坐标;
(2)点![]() 是线段
是线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,连接
,连接![]() .若点
.若点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在
恰好在![]() 轴上,求出点
轴上,求出点![]() 的坐标;
的坐标;
(3)在平面内是否存在一点![]() ,使
,使![]() 关于点
关于点![]() 的对称
的对称![]() (点
(点![]() ,
,![]() ,
,![]() 分别是点
分别是点![]() ,
,![]() ,
,![]() 的对称点)恰好有两个顶点落在该抛物线上?若存在,求出点
的对称点)恰好有两个顶点落在该抛物线上?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )
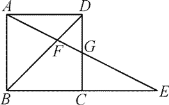
A. 6B. 8
C. 10D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育部基础教育司负责人解读“2020新中考”时强调要注重学生分析与解决问题的能力,要增强学生的创新精神和综合素质.王老师想尝试改变教学方法,将以往教会学生做题改为引导学生会学习.于是她在菱形的学习中,引导同学们解决菱形中的一个问题时,采用了以下过程(请解决王老师提出的问题):
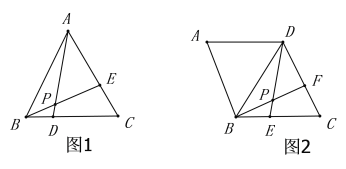
先出示问题(1):如图1,在等边三角形![]() 中,
中,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 上一点,如果
上一点,如果![]() ,连接
,连接![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,求
,求![]() 的度数.
的度数.
通过学习,王老师请同学们说说自己的收获.小明说发现一个结论:在这个等边三角形![]() 中,只要满足
中,只要满足![]() ,则
,则![]() 的度数就是一个定值,不会发生改变.紧接着王老师出示了问题(2):如图2,在菱形
的度数就是一个定值,不会发生改变.紧接着王老师出示了问题(2):如图2,在菱形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 上一点,
上一点,![]() ,连接
,连接![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,如果
,如果![]() ,
,![]() ,求出菱形的边长.
,求出菱形的边长.
问题(3):通过以上的学习请写出你得到的启示(一条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点B的坐标为![]() ,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数
,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数![]() 的图象交AB,BC分别于点E,F.
的图象交AB,BC分别于点E,F.
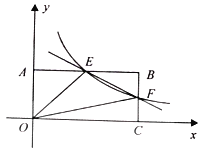
(1)求直线EF的解析式.
(2)求四边形BEOF的面积.
(3)若点P在y轴上,且![]() 是等腰三角形,请直接写出点P的坐标.
是等腰三角形,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com