
【题目】如图,在平面直角坐标系 ![]() 中,矩形
中,矩形 ![]() 的边
的边 ![]() 在
在 ![]() 轴上,顶点
轴上,顶点 ![]() 在抛物线
在抛物线 ![]() 上,且抛物线交
上,且抛物线交 ![]() 轴于另一点
轴于另一点 ![]() .
.
(1)则 ![]() = ,
= , ![]() =;
=;
(2)已知 ![]() 为
为 ![]() 边上一个动点(不与
边上一个动点(不与 ![]() 、
、 ![]() 重合),连结
重合),连结 ![]() 交
交 ![]() 于点
于点 ![]() ,过点
,过点 ![]() 作
作 ![]() 轴的平行线分别交抛物线、直线
轴的平行线分别交抛物线、直线 ![]() 于
于 ![]() 、
、 ![]() .
.
①求线段 ![]() 的最大值,此时
的最大值,此时 ![]() 的面积为;
的面积为;
②若以点 ![]() 为圆心,
为圆心, ![]() 为半径作⊙O,试判断直线
为半径作⊙O,试判断直线 ![]() 与⊙O的能否相切,若能请求出
与⊙O的能否相切,若能请求出 ![]() 点坐标,若不能请说明理由.
点坐标,若不能请说明理由.
【答案】
(1)![]() ,
,![]()
(2)解:①由点O(0,0)、B(4,2)两点可得直线OB的解析式为 ![]() ,
,
设点E的坐标为(m,2),则点F的坐标为(m, ![]() ),点G的坐标为(m,
),点G的坐标为(m, ![]() ),∴FG=(
),∴FG=( ![]() )-
)- ![]() =
= ![]() ,
,
∴当m=2时,线段FG的最大值为1.
此时过E(2,2)、A(4,0)两点直线AE的解析式为y=-x+4,
∴直线OB与直线AE的交点P的坐标为( ![]() ,
, ![]() ),
),
∴ ![]() 边FG边上的高为
边FG边上的高为 ![]() ,
,
∴ ![]() 的面积为
的面积为 ![]() ;②直线AE能与⊙O相切,当直线AE与⊙O相切时,则OB⊥AE,∴△ABE∽△OAB,
;②直线AE能与⊙O相切,当直线AE与⊙O相切时,则OB⊥AE,∴△ABE∽△OAB,
∴ ![]() ,即
,即 ![]() ,
,
∴BE=1,CE=3,
∴点E的坐标为(3,2).
【解析】(1)把点B与点D坐标代入抛物线解析式,建立方程,求出a与b的值即可。
(2)①先求出直线OB的解析式,设出E坐标为(m,2),根据EG与y轴平行,表示出F与G坐标,进而表示出FG,,列出FG关于x的函数解析式,利用二次函数性质求出FG最大值,以及此时m的值,确定出E坐标,利用待定系数法求出直线AE解析式,与直线OB联立求出交点P坐标,进而确定出此时三角形PFG面积即可;②当AE⊥OB,垂足为P时,以点O为圆心,OP为半径作 O,直线AE与 O相切,如图所示,根据直线OB解析式确定出直线AE解析式,进而求出垂足P坐标,再证明△ABE∽△OAB,根据相似三角形的性质求出AE、BE的长,即可求出点E的坐标。
【考点精析】关于本题考查的二次函数的最值和相似三角形的判定与性质,需要了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,AD=![]() ,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
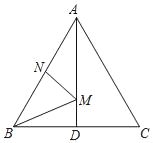
A. ![]() B. 2C. 1D. 3
B. 2C. 1D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点![]() 在
在![]() 轴正半轴,点
轴正半轴,点![]() 在
在![]() 轴负半轴,连接
轴负半轴,连接![]() ,
,![]() ,
,![]()
(1)求点![]() 坐标
坐标
(2)如图2,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为直角边做等腰直角
为直角边做等腰直角![]() ,
,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(3)在(2)的条件下,如图3,在![]() 延长线上有一点
延长线上有一点![]() ,过点
,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD.
(1)求证:∠1+∠2=90°;
(2)若∠ABD的平分线与CD的延长线交于F,且∠F=55°,求∠ABC;
(3)若H是BC上一动点,F是BA延长线上一点,FH交BD于M,FG平分∠BFH,交DE于N,交BC于G.当H在BC上运动时(不与B点重合),试判断∠BAD+∠DMH与∠DNG的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),C(﹣1,2),且![]() .
.
(1)求a,b的值;
(2)y轴上是否存在一点M,使△COM的面积是△ABC的面积的一半,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在3×3的方格中,点A、B、C、D、E、F都是格点,从A、D、E、F四点中任意取一点,以所取点及B、C为顶点画三角形,所画三角形是直角三角形的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
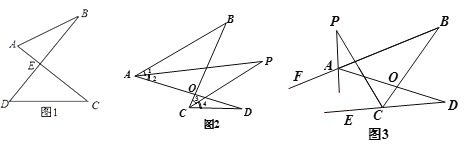
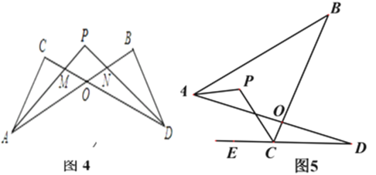
【题目】(问题背景)
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
(简单应用)
(2)如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=46°,∠ADC=26°,求∠P的度数;
(问题探究)
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
(拓展延伸)
(4) ①在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为: (用α、β表示∠P);
∠CDB,试问∠P与∠C、∠B之间的数量关系为: (用α、β表示∠P);
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE, 猜想∠P与∠B、∠D的关系,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形ABC在平面直角坐标系中的位置如图所示.将三角形ABC向右平移6个单位长度,再向下平移6个单位长度得到三角形A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的三角形A1B1C1;
(2)求三角形ABC的面积;
(3)直接写出三角形A1B1C1各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
编号 类型 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(1) 计算甲、乙两种电子钟走时误差的平均数;
(2) 计算甲、乙两种电子钟走时误差的方差;
(3) 根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com