
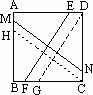
如图所示,正方形ABCD中,E、M、F、N分别是AD、AB、BC、CD上的点,若EF⊥MN.求证:EF=MN.
|
证明:如图,作DG∥EF交BC于G,作CH∥MN交AB于H. ∵CH∥MN,DG∥EF,EF⊥MN,∴CH⊥DG. 又∵DC⊥BC,∴∠BCH=∠CDG. ∵BC=CD,∠HBC=∠GCD,∴△BCH≌△CDG. ∴CH=DG.又∵AD∥BC,DG∥EF, ∴四边形EFGD为平行四边形,∴EF=DG. 同理CH=MN,∴MN=EF. 解析:解答本题的关键是如何将条件和问题很好地结合起来.EF、MN的位置较孤立,不妨分别过D、C作DG∥EF、CH∥MN,将问题一步步转化,来证明结论. 说明:①本题实际上是平行移动法,经常利用这一方法将条件和问题相对集中. ②本题还可分别过E、N作CD、BC的平行线来解决. |


科目:初中数学 来源: 题型:
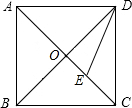 如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )
如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是
如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com