
一条抛物线![]() 经过点
经过点![]() 与
与![]() .
.
(1)求这条抛物线的解析式,并写出它的顶点坐标;
(2)现有一半径为1、圆心![]() 在抛物线上运动的动圆,当⊙
在抛物线上运动的动圆,当⊙![]() 与坐标轴相切时,求圆心
与坐标轴相切时,求圆心![]() 的坐标;
的坐标;
(3)⊙![]() 能与两坐标轴都相切吗?如果不能,试通过上下平移抛物线
能与两坐标轴都相切吗?如果不能,试通过上下平移抛物线![]() 使⊙
使⊙![]() 与两坐标轴都相切(要说明平移方法).
与两坐标轴都相切(要说明平移方法).

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
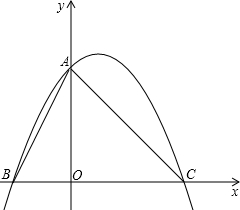
查看答案和解析>>
科目:初中数学 来源: 题型:
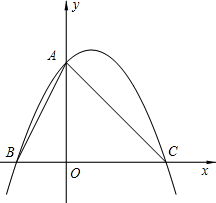 ,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).
,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).查看答案和解析>>
科目:初中数学 来源:第27章《二次函数》中考题集(28):27.3 实践与探索(解析版) 题型:解答题
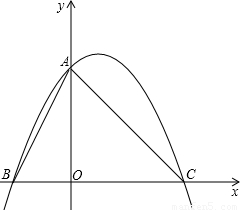
查看答案和解析>>
科目:初中数学 来源:2011年四川省凉山州盐源县民族中学中考数学一模试卷(解析版) 题型:解答题
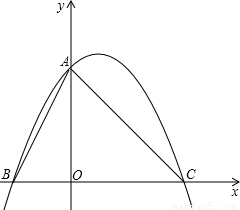
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com