
【题目】如图,![]() 和
和![]() 都是等边三角形,下列结论:①
都是等边三角形,下列结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() ;其中正确的有( )个
;其中正确的有( )个
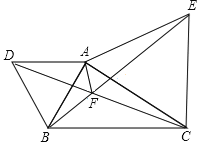
A.2B.3C.4D.1
【答案】B
【解析】
利用△ADC≌△ABE(SAS),即可推出①③正确,在DF上取一点K,使得FK=FA,可得△AKF是等边三角形,由△DAK≌△BAF,推出④正确,想办法证明AF平分∠DFE,显然AF平分∠BAC不成立,推出②错误;
如图设AC交BE于点O.
∵△ABD,△ACE都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°,
∴∠DAC=∠BAE
∴△ADC≌△ABE(SAS),
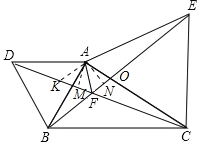
∴CD=BE,∠AEO=∠OCN,故①正确
作AM⊥CD于M,AN⊥BE于N,
∵△ADC≌△ABE,
∴AM=AN,
∵AM⊥CD于M,AN⊥BE于N,
∴AF平分∠DFE,无法判断AF平分∠BAC,故②错误,
∵∠AOE=∠COF,
∴∠OAE=∠OFC=60°,
∴∠BFC=120°,故③正确,
在DF上取一点K,使得FK=FA,
∵∠AFK=∠AFN=60°,
∴△AKF是等边三角形,
易证△DAK≌△BAF,
∴DK=BF,
∴DF=DK+KF=FA+FB,故④正确,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
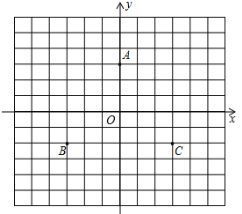
(1)图中点![]() 的坐标是________.
的坐标是________.
(2)点![]() 关于
关于![]() 轴对称的点
轴对称的点![]() 的坐标是______,并作出四边形
的坐标是______,并作出四边形![]() .
.
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=7,AC=6,∠A=45°,点D、E分别在边AB、BC上,将△BDE沿着DE所在直线翻折,点B落在点P处,PD、PE分别交边AC于点M、N,如果AD=2,PD⊥AB,垂足为点D,那么MN的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.
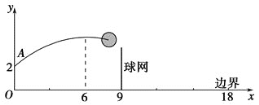
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(4![]() ,0)、(0,4),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的纵坐标为( )
,0)、(0,4),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的纵坐标为( )

A. ![]() +1 B.
+1 B. ![]() -1 C. 2
-1 C. 2![]() +3 D. 2
+3 D. 2![]() +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4 经过点A(﹣3,0),点 B 在抛物线上,CB∥x轴,且AB 平分∠CAO.则此抛物线的解析式是___________.
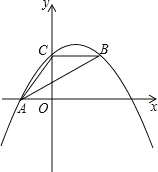
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
已知:如图(1),在平面直角坐标系中,点![]() ,
,![]() ,
,![]() 分别在坐标轴上,且
分别在坐标轴上,且![]() ,
,![]() 的面积为
的面积为![]() ,点
,点![]() 从
从![]() 点出发沿
点出发沿![]() 轴负方向以
轴负方向以![]() 个单位长度/秒的速度向下运动,连接
个单位长度/秒的速度向下运动,连接![]() ,
,![]() ,点
,点![]() 为
为![]() 上的中点.
上的中点.
(1)直接写出坐标![]() ___________,
___________,![]() ___________,
___________,![]() ___________.
___________.
(2)设点![]() 运动的时间为
运动的时间为![]() 秒,问:当
秒,问:当![]() 与
与![]() 垂直且相等时,求此时
垂直且相等时,求此时![]() 的值?并说明理由.
的值?并说明理由.
(3)如图(2)![]() ,在第四象限内有一动点
,在第四象限内有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,点
,点![]() 在第四象限内运动,当
在第四象限内运动,当![]() ,判断
,判断![]() 是否平分
是否平分![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com