
 如图,点C在线段AB上,AC=6cm,MB=10cm,点M,N分别为AC,BC的中点.
如图,点C在线段AB上,AC=6cm,MB=10cm,点M,N分别为AC,BC的中点.分析 (1)根据“点M、N分别是AC、BC的中点”,先求出MC、CN的长度,再利用BC=MB-MC,MN=CM+CN即可求出线段BC,MN的长度即可.
(2)先画图,再根据线段中点的定义得MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC,然后利用MN=MC-NC得到MN=$\frac{1}{2}$acm.
解答 解:(1)∵M是AC的中点,
∴MC=$\frac{1}{2}$AC=3cm,
∴BC=MB-MC=7cm,
又N为BC的中点,
∴CN=$\frac{1}{2}$BC=3.5cm,
∴MN=MC+NC=6.5cm;
(2)如图: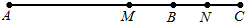
∵M是AC的中点,
∴CM=$\frac{1}{2}$AC,
∵N是BC的中点,
∴CN=$\frac{1}{2}$BC,
∴MN=CM-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$acm.
点评 本题主要考查了两点间的距离,线段的中点定义,线段的中点把线段分成两条相等的线段.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.
小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
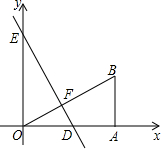 如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点D、E,交OB于点F.
如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点D、E,交OB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com