
【题目】在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() 是
是![]() 上的一点(不与点
上的一点(不与点![]() 重合),
重合),![]() 于点
于点![]() .
.
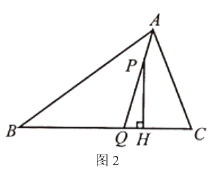
(1)若![]() ,如图1,当点
,如图1,当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的度数;
的度数;

(2)当![]() 是锐角三角形时,如图2,试探索
是锐角三角形时,如图2,试探索![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)150°;(2)![]() ,见解析
,见解析
【解析】
(1)由三角形的内角和得到∠BAC=180°60°30°=90°,根据角平分线定义得到∠BAQ=∠QAC=![]() ∠BAC=45°,由垂直的定义得到∠PHQ=90°,于是得到∠QPH=∠QAH=90°75°=15°;
∠BAC=45°,由垂直的定义得到∠PHQ=90°,于是得到∠QPH=∠QAH=90°75°=15°;
(2)如图2,过A作AG⊥BC于G,得到∠PHQ=∠AGQ=90°,根据平行线的性质得到∠QPH=∠QAG,设∠QPH=∠QAG=x,根据角平分线的定义得到∠BAQ=∠QAC=x+∠GAC,列方程即可得到结论.
解:![]() ,
,
![]() ,
,![]() .
.
![]() 平分
平分![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]() 如图,过点
如图,过点![]() 作
作![]() 于点
于点![]() ,
,
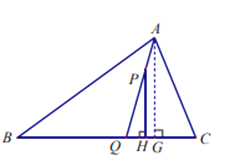
则![]() ,
,
![]()
![]()
设![]()
![]() 平分
平分![]()
img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/27/16/37948ee7/SYS202011271638291059812140_DA/SYS202011271638291059812140_DA.023.png" width="206" height="22" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
![]()
又![]()
![]() .
.
![]()
![]()
![]() ,
,
![]()
![]() 即
即![]() .
.


科目:初中数学 来源: 题型:
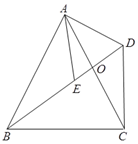
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别标有数字1、2、3的三张卡片洗匀后,背面朝上放在桌面上请完成下列各题
(1)随机抽取1张,求抽到卡片数字是奇数的概率;
(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?
(3)在(2)的条件下,试求组成的两位数是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由不同生产商提供![]() 套校服参加比选,甲、乙、两三个同学分别参加比选,比选后结果是:每套校服至少有一人选中,且每人都选中了其中的
套校服参加比选,甲、乙、两三个同学分别参加比选,比选后结果是:每套校服至少有一人选中,且每人都选中了其中的![]() 套校服.如果将其中只有
套校服.如果将其中只有![]() 人选中的校服称作“不受欢迎校服”,
人选中的校服称作“不受欢迎校服”,![]() 人选中的校服称作“颇受欢迎校服”,
人选中的校服称作“颇受欢迎校服”,![]() 人都选中的校服称作“最受欢迎校服”,则“不受欢迎校服”比“最受欢迎校服”多________________套.
人都选中的校服称作“最受欢迎校服”,则“不受欢迎校服”比“最受欢迎校服”多________________套.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一节前夕,某商店从厂家购进![]() 两种礼盒,已知
两种礼盒,已知![]() 两种礼盒的单价比为
两种礼盒的单价比为![]() ,单价和为
,单价和为![]() 元
元
(1)求![]() 两种礼盒的单价分别是多少元?
两种礼盒的单价分别是多少元?
(2)该商店购进这两种礼盒恰好用去![]() 元,且购进
元,且购进![]() 种礼盒最多
种礼盒最多![]() 个,
个,![]() 种礼盒的数量不超过
种礼盒的数量不超过![]() 种礼盒数量的
种礼盒数量的![]() 倍,共有哪几种进货方案?
倍,共有哪几种进货方案?
(3)根据市场行情,销售一个![]() 种礼盒可获利
种礼盒可获利![]() 元,销售一个
元,销售一个![]() 种礼盒可获利
种礼盒可获利![]() 元.为奉献爱心,该商店决定每售出一个
元.为奉献爱心,该商店决定每售出一个![]() 种礼盒,为爱心公益基金捐款
种礼盒,为爱心公益基金捐款![]() 元,每个
元,每个![]() 种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,
种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,![]() 的值是多少?此时该商店可获利多少元?
的值是多少?此时该商店可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
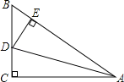
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论.①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD 和折线 OABC 表示“龟兔赛跑”时的路程与时间关系,请你根据图中给出的信息,解决下列问题:
(1)折线 OABC 表示赛跑过程中_______的路程与时间的关系, 线段 OD 表示赛跑过程中_______的路程与时间的关系, 赛跑的全程是________米.
(2)兔子在起初每分钟跑多少米,乌龟用多少分钟追上了正在睡觉的兔子.
(3)兔子醒来,以 48 千米/小时的速度跑向终点,结果还是比乌龟晚到 0.5 分钟,请你算算兔子中间停下睡觉用了多少分钟?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com