解:∵
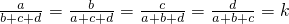
,
∴a=(b+c+d)k,①
b=(a+c+d)k,②
c=(a+b+d)k,③
d=(a+b+c)k,④
∴①+②+③+④得,a+b+c+d=k(3a+3b+3c+3d),
当a+b+c+d=0时,
∴b+c+d=-a,
∵a=(b+c+d)k,
∴a=-ak
∴k=-1,
当a+b+c+d≠0时,∴两边同时除以a+b+c+d得,3k=1,
∴k=

.
故答案为:k=-1或

.
分析:根据已知条件得a=(b+c+d)k①,b=(a+c+d)k②,c=(a+b+d)k③,d=(a+b+c)k④,将①②③④相加,分a+b+c+d=0与不等于0两种情况讨论,所以k有两个解.
点评:本题考查了分式的混合运算,以及分式的基本性质,比较简单要熟练掌握.

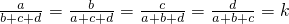 ,试求k的值.
,试求k的值.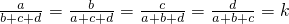 ,
, .
. .
.

 阅读快车系列答案
阅读快车系列答案