
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
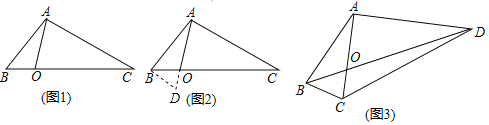
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
【答案】(1)75;4![]() ;(2)CD=4
;(2)CD=4![]() .
.
【解析】(1)根据平行线的性质可得出∠ADB=∠OAC=75°,结合∠BOD=∠COA可得出△BOD∽△COA,利用相似三角形的性质可求出OD的值,进而可得出AD的值,由三角形内角和定理可得出∠ABD=75°=∠ADB,由等角对等边可得出AB=AD=4![]() ,此题得解;
,此题得解;
(2)过点B作BE∥AD交AC于点E,同(1)可得出AE=4![]() ,在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解.
,在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解.
(1)∵BD∥AC,
∴∠ADB=∠OAC=75°.
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴![]() .
.
又∵AO=3![]() ,
,
∴OD=![]() AO=
AO=![]() ,
,
∴AD=AO+OD=4![]() .
.
∵∠BAD=30°,∠ADB=75°,
∴∠ABD=180°-∠BAD-∠ADB=75°=∠ADB,
∴AB=AD=4![]() .
.
(2)过点B作BE∥AD交AC于点E,如图所示.
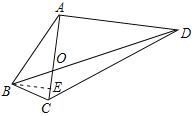
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°.
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴![]() .
.
∵BO:OD=1:3,
∴![]() .
.
∵AO=3![]() ,
,
∴EO=![]() ,
,
∴AE=4![]() .
.
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
∴AB=2BE.
在Rt△AEB中,BE2+AE2=AB2,即(4![]() )2+BE2=(2BE)2,
)2+BE2=(2BE)2,
解得:BE=4,
∴AB=AC=8,AD=12.
在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,
解得:CD=4![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
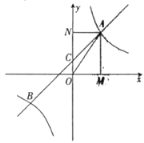
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一、三象限内的
的图象交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,过点
点,过点![]() 作
作![]() 轴于点
轴于点![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求四边形![]() 的周长和面积.
的周长和面积.
(2)求该反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
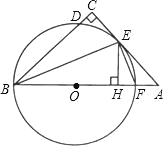
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
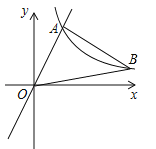
【题目】(2017山东省日照市)如图,在平面直角坐标系中,经过点A的双曲线![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则k的值为______.
,∠AOB=∠OBA=45°,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢,现在小明让小亮先跑若干米,两人的路程![]() (米)分别与小明追赶时间
(米)分别与小明追赶时间![]() (秒)的函数关系如图所示。
(秒)的函数关系如图所示。
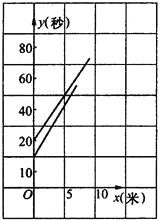
⑴小明让小亮先跑了多少米?
⑵分别求出表示小明、小亮的路程与时间的函数关系式。
⑶谁将赢得这场比赛?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
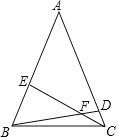
【题目】如图,在ABC中,AB=AC=10,E,D分别是AB,AC上的点,BE=4,CD=2,且BD=CE,则BD=________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
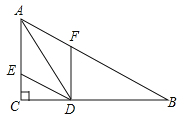
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com