
分析 对题目中的式子先化简,再合并同类项,即可得到问题的答案.
解答 解:(1)3$\sqrt{18}$+$\frac{\sqrt{50}}{5}$-4$\sqrt{0.5}$
=$9\sqrt{2}+\frac{5\sqrt{2}}{5}-4×\frac{\sqrt{2}}{2}$
=$9\sqrt{2}+\sqrt{2}-2\sqrt{2}$
=$8\sqrt{2}$;
(2)$\sqrt{27}$-15$\sqrt{\frac{1}{3}}$+$\frac{1}{4}$$\sqrt{48}$
=$3\sqrt{3}-15×\frac{\sqrt{3}}{3}+\frac{1}{4}×4\sqrt{3}$
=$3\sqrt{3}-5\sqrt{3}+\sqrt{3}$
=-$\sqrt{3}$;
(3)$\sqrt{6}$-$\sqrt{\frac{3}{2}}$-$\sqrt{\frac{2}{3}}$+$\sqrt{48}$-$\sqrt{12}$
=$\sqrt{6}-\frac{\sqrt{6}}{2}-\frac{\sqrt{6}}{3}+4\sqrt{3}-2\sqrt{3}$
=$\frac{\sqrt{6}}{6}+2\sqrt{3}$.
点评 本题考查二次根式的加减法,解题的关键是将二次根式要化到最简.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳老河口九年级3月月考数学试卷(解析版) 题型:解答题
如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF.
(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长.
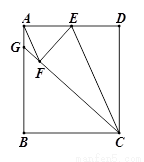
查看答案和解析>>
科目:初中数学 来源:2017届江苏省连云港市灌云县西片九年级下学期第一次月考数学试卷(解析版) 题型:判断题
如图,抛物线y=﹣x2+2x+3,与坐标轴交于点A,B,C,且D为抛物线的顶点.
(1)求出点A,B,C,D的坐标:填空A( ),B( ),C( ),D( )。
(2)点C关于抛物线y=﹣x2+2x+3对称轴的对称点为E点,联结BC,BE,求∠CBE的正切值;
(3)点M是抛物线对称轴上一点,且△DMB和△BCE相似,求点M坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm,3cm,5cm | B. | 1cm,1cm,2cm | C. | 1cm,2cm,3cm | D. | 1cm,2cm,2cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com