
【题目】如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
(1)当t= _________ s时,点P与点Q重合;
(2)当t= _________ s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.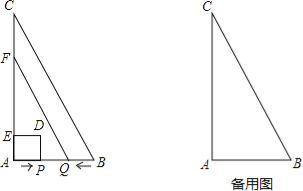
【答案】(1)1 (2)![]() (3)
(3)
【解析】
试题(1)当点P与点Q重合时,AP=BQ=t,且AP+BQ=AB=2,
∴t+t=2,解得t=1s,
故填空答案:1.
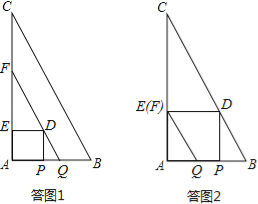
(2)当点D在QF上时,如答图1所示,此时AP=BQ=t.
∵QF∥BC,APDE为正方形,∴△PQD∽△ABC,
∴DP:PQ=AC:AB=2,则PQ=![]() DP=
DP=![]() AP=
AP=![]() t.
t.
由AP+PQ+BQ=AB=2,得t+![]() t+t=2,解得:t=
t+t=2,解得:t=![]() .
.
故填空答案:![]() .
.
(3)当P、Q重合时,由(1)知,此时t=1;
当D点在BC上时,如答图2所示,此时AP=BQ=t,BP=![]() t,求得t=
t,求得t=![]() s,进一步分析可知此时点E与点F重合;
s,进一步分析可知此时点E与点F重合;
当点P到达B点时,此时t=2.
因此当P点在Q,B两点之间(不包括Q,B两点)时,其运动过程可分析如下:
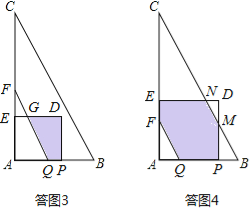
①当1<t≤![]() 时,如答图3所示,此时重合部分为梯形PDGQ.
时,如答图3所示,此时重合部分为梯形PDGQ.
此时AP=BQ=t,∴AQ=2﹣t,PQ=AP﹣AQ=2t﹣2;
易知△ABC∽△AQF,可得AF=2AQ,EF=2EG.
∴EF=AF﹣AE=2(2﹣t)﹣t=4﹣3t,EG=![]() EF=2﹣
EF=2﹣![]() t,
t,
∴DG=DE﹣EG=t﹣(2﹣![]() t)=
t)=![]() t﹣2.
t﹣2.
S=S梯形PDGQ=![]() (PQ+DG)PD=
(PQ+DG)PD=![]() [(2t﹣2)+(
[(2t﹣2)+(![]() t﹣2)]t=
t﹣2)]t=![]() t2﹣2t;
t2﹣2t;
②当![]() <t<2时,如答图4所示,此时重合部分为一个多边形.
<t<2时,如答图4所示,此时重合部分为一个多边形.
此时AP=BQ=t,∴AQ=PB=2﹣t,
易知△ABC∽△AQF∽△PBM∽△DNM,可得AF=2AQ,PM=2PB,DM=2DN,
∴AF=4﹣2t,PM=4﹣2t.
又DM=DP﹣PM=t﹣(4﹣2t)=3t﹣4,∴DN=![]() (3t﹣4).
(3t﹣4).
S=S正方形APDE﹣S△AQF﹣S△DMN=AP2﹣![]() AQAF﹣
AQAF﹣![]() DNDM
DNDM
=t2﹣![]() (2﹣t)(4﹣2t)﹣
(2﹣t)(4﹣2t)﹣![]() ×
×![]() (3t﹣4)×(3t﹣4)
(3t﹣4)×(3t﹣4)
=﹣![]() t2+10t﹣8.
t2+10t﹣8.
综上所述,当点P在Q,B两点之间(不包括Q,B两点)时,S与t之间的函数关系式为:
S= .
.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】某农场要建一个长方形的养鸡场,鸡场的一边靠长为18m的墙,另三边用木栏围城,木栏长为32m.

(1)鸡场的面积能围成120m2吗?
(2)鸡场的面积能围成130m2吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习反比例函数的图象时,他的老师要求同学们根据“探索一次函数y1=x+1的图象”的基本步骤,在纸上逐步探索函数y2=![]() 的图象,并且在黑板上写出4个点的坐标:A(
的图象,并且在黑板上写出4个点的坐标:A(![]() ,
,![]() ),B(1,2),C(1,
),B(1,2),C(1,![]() ),D(﹣2,﹣1).
),D(﹣2,﹣1).
(1)在A、B、C、D四个点中,任取一个点,这个点既在直线y1=x+1又在双曲线y2=![]() 上的概率是多少?
上的概率是多少?
(2)小明从A、B、C、D四个点中任取两个点进行描点,求两点都落在双曲线y2=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)关于x,y的方程组![]() 满足x+y=5,求m的值.
满足x+y=5,求m的值.
(2)关于x的一元二次方程x2﹣(m﹣1)x﹣m=0的两个根x1,x2满足x12+x22=5,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=2![]() ,CD=
,CD=![]() ,点P在四边形ABCD的边上.若P到BD的距离为
,点P在四边形ABCD的边上.若P到BD的距离为![]() ,则点P的个数为( )
,则点P的个数为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在5天中进球的个数统计如果如下:队员每人每天进球数(个)经过计算,甲进球的平均数为x甲=8和方差S2甲=3.2.

(1)求乙进球的平均数x乙和方差S2乙;
(2)现在需要根据以上数据,从甲、乙二人中选出一人去参加3分球投篮大赛,你认为应该选哪名队员?说说你的理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
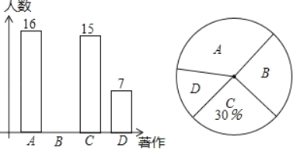
【题目】某校对A《唐诗》、B《宋词》、C《蒙山童韵》、D其它,这四类著作开展“最受欢迎的传统文化著作”调查,随机调查了若干名学生(每名学生必选且只能选这四类著作中的一种)并将得到的信息绘制了下面两幅不完整的统计图:
(1)求一共调查了多少名学生;
(2)请将条形统计图补充完整;
(3)该校语文老师想从这四类著作中随机选取两类作为学生寒假必读书籍,请用树状图或列表的方法求恰好选中《宋词》和《蒙山童韵》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() .动点
.动点![]() ,
,![]() 同时从点
同时从点![]() 出发,
出发,![]() 沿
沿![]() ,
,![]() 沿折线
沿折线![]() ,均以每秒1个单位长度的速度移动,当一个动点到达终点
,均以每秒1个单位长度的速度移动,当一个动点到达终点![]() 时,另一个动点也随之停止移动,移动时间记为
时,另一个动点也随之停止移动,移动时间记为![]() 秒,连接
秒,连接![]() .
.
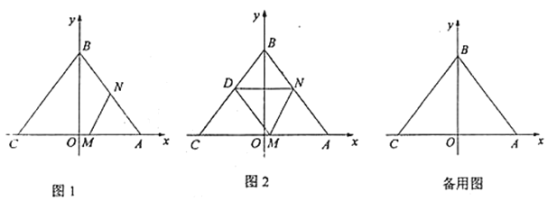
(Ⅰ)如图1,当点![]() 移动到
移动到![]() 中点时,求此时
中点时,求此时![]() 的值及
的值及![]() 点坐标;
点坐标;
(Ⅱ)在移动过程中,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 的对称点为
的对称点为![]() .
.
①如图2,当点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处时,求此时
处时,求此时![]() 的值;
的值;
②当点![]() 移动到点
移动到点![]() 时,点
时,点![]() 落在点
落在点![]() 处,求此时点
处,求此时点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com