
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬![]() өД¶ҘөгЧшұк·ЦұрОӘ
өД¶ҘөгЧшұк·ЦұрОӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .¶Ҝөг
.¶Ҝөг![]() Ј¬
Ј¬![]() Н¬КұҙУөг
Н¬КұҙУөг![]() іц·ўЈ¬
іц·ўЈ¬![]() СШ
СШ![]() Ј¬
Ј¬![]() СШХЫПЯ
СШХЫПЯ![]() Ј¬ҫщТФГҝГл1ёцөҘО»іӨ¶ИөДЛЩ¶ИТЖ¶ҜЈ¬өұТ»ёц¶ҜөгөҪҙпЦХөг
Ј¬ҫщТФГҝГл1ёцөҘО»іӨ¶ИөДЛЩ¶ИТЖ¶ҜЈ¬өұТ»ёц¶ҜөгөҪҙпЦХөг![]() КұЈ¬БнТ»ёц¶ҜөгТІЛжЦ®НЈЦ№ТЖ¶ҜЈ¬ТЖ¶ҜКұјдјЗОӘ
КұЈ¬БнТ»ёц¶ҜөгТІЛжЦ®НЈЦ№ТЖ¶ҜЈ¬ТЖ¶ҜКұјдјЗОӘ![]() ГлЈ¬Б¬ҪУ
ГлЈ¬Б¬ҪУ![]() .
.
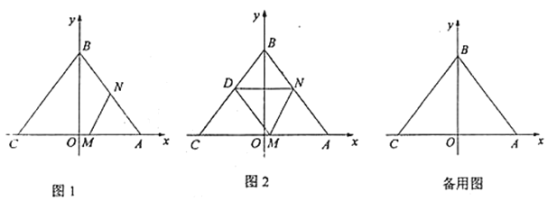
ЈЁўсЈ©ИзНј1Ј¬өұөг![]() ТЖ¶ҜөҪ
ТЖ¶ҜөҪ![]() ЦРөгКұЈ¬ЗуҙЛКұ
ЦРөгКұЈ¬ЗуҙЛКұ![]() өДЦөј°
өДЦөј°![]() өгЧшұкЈ»
өгЧшұкЈ»
ЈЁўтЈ©ФЪТЖ¶Ҝ№эіМЦРЈ¬Ҫ«![]() СШЦұПЯ
СШЦұПЯ![]() ·ӯХЫЈ¬өг
·ӯХЫЈ¬өг![]() өД¶ФіЖөгОӘ
өД¶ФіЖөгОӘ![]() .
.
ўЩИзНј2Ј¬өұөг![]() ЗЎәГВдФЪ
ЗЎәГВдФЪ![]() ұЯЙПөДөг
ұЯЙПөДөг![]() ҙҰКұЈ¬ЗуҙЛКұ
ҙҰКұЈ¬ЗуҙЛКұ![]() өДЦөЈ»
өДЦөЈ»
ўЪөұөг![]() ТЖ¶ҜөҪөг
ТЖ¶ҜөҪөг![]() КұЈ¬өг
КұЈ¬өг![]() ВдФЪөг
ВдФЪөг![]() ҙҰЈ¬ЗуҙЛКұөг
ҙҰЈ¬ЗуҙЛКұөг![]() өДЧшұкЈЁЦұҪУРҙіцҪб№ыјҙҝЙЈ©.
өДЧшұкЈЁЦұҪУРҙіцҪб№ыјҙҝЙЈ©.
Ўҫҙр°ёЎҝЈЁўсЈ©![]() ,өг
,өг![]() ЧшұкОӘ
ЧшұкОӘ![]() ; ЈЁўтЈ©ўЩ
; ЈЁўтЈ©ўЩ![]() ; ўЪ
; ўЪ![]() өгЧшұкОӘ
өгЧшұкОӘ![]()
ЎҫҪвОцЎҝ
(1)ёщҫЭөгөДЧшұкЈ¬ТФЗуөГABөДіӨЈ¬УЙУЪNКЗABөДЦРөгЈ¬ҝЙөГANөДіӨ¶ИЈ¬ҙУ¶шЗуіцtЈ¬јҙҝЙЗуMөгәъЧшұк;
(2)ўЩУЙ·ӯЧЕөДРФЦКҝЙөГЛДұЯРО![]() ОӘБвРОЈ¬ФтУР
ОӘБвРОЈ¬ФтУР![]() ЦбЈ¬ҝЙөГөҪ
ЦбЈ¬ҝЙөГөҪ![]() Ј¬јҙ
Ј¬јҙ![]() Ј¬ҙУ¶шЗуіцt.
Ј¬ҙУ¶шЗуіцt.
ўЪёщҫЭПаЛЖҝЙТФЗуіцN(![]() )Ј¬ЙиE(x,y),ёщҫЭ№ҙ№Й¶ЁАнБРіц·ҪіМЧй:EM=6,EN=5,ҪвөГјҙҝЙЗуіцөгE.
)Ј¬ЙиE(x,y),ёщҫЭ№ҙ№Й¶ЁАнБРіц·ҪіМЧй:EM=6,EN=5,ҪвөГјҙҝЙЗуіцөгE.
ЈЁўсЈ©ЎЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬![]() Ј¬Ўа
Ј¬Ўа![]() .
.
өұөг![]() ТЖ¶ҜөҪ
ТЖ¶ҜөҪ![]() ЦРөгКұЈ¬УЙМвТвҝЙөГ
ЦРөгКұЈ¬УЙМвТвҝЙөГ![]() Ј¬
Ј¬
Ўа![]() .
.
ЎЯ![]() Ј¬
Ј¬
Ўаөг![]() ЧшұкОӘ
ЧшұкОӘ![]() .
.
ЈЁўтЈ©ўЩУЙМвТвҝЙөГ![]() Ј¬
Ј¬
ЎЯ![]() СШЦұПЯ
СШЦұПЯ![]() ·ӯХЫЈ¬өг
·ӯХЫЈ¬өг![]() ВдФЪөг
ВдФЪөг![]() ҙҰЈ¬
ҙҰЈ¬
Ўа![]() Ј¬
Ј¬
ЎаЛДұЯРО![]() ОӘБвРОЈ¬
ОӘБвРОЈ¬
Ўа![]() Ј¬
Ј¬![]() ЦбЈ¬
ЦбЈ¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬![]() Ј¬
Ј¬
ҪвөГ![]() .
.
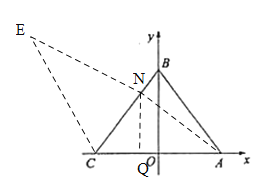
ЈЁўтЈ©ўЪ№эNЧцXЦбөДҙ№ПЯЈ¬ҙ№ЧгОӘQЈ¬УЙЎчCNQЎЧЎчBCOЈ¬
УЦЎЯBN=1,AC=6,BC=5,
Ўа![]() ,ЎаN(
,ЎаN(![]() )Ј¬
)Ј¬
ЙиE(x,y),ЗТCE=6,EN=5,
Фт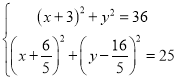
ҪвөГЈә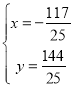
![]() өгЧшұкОӘ
өгЧшұкОӘ![]() .
.


 ЖЪД©ёҙП°јмІвПөБРҙр°ё
ЖЪД©ёҙП°јмІвПөБРҙр°ё і¬ДЬС§өдөҘФӘЖЪЦРЖЪД©ЧЁМвіеҙМ100·ЦПөБРҙр°ё
і¬ДЬС§өдөҘФӘЖЪЦРЖЪД©ЧЁМвіеҙМ100·ЦПөБРҙр°ё »ЖёФ360¶И¶ЁЦЖГЬҫнПөБРҙр°ё
»ЖёФ360¶И¶ЁЦЖГЬҫнПөБРҙр°ё Сф№вҝјіЎөҘФӘІвКФҫнПөБРҙр°ё
Сф№вҝјіЎөҘФӘІвКФҫнПөБРҙр°ё ГыРЈБӘГЛіеҙМҫнПөБРҙр°ё
ГыРЈБӘГЛіеҙМҫнПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎчABCЦРЈ¬ЎПA=90ЎгЈ¬AB=2cmЈ¬AC=4cmЈ®¶ҜөгPҙУөгAіц·ўЈ¬СШAB·ҪПтТФ1cm/sөДЛЩ¶ИПтөгBФЛ¶ҜЈ¬¶ҜөгQҙУөгBН¬Кұіц·ўЈ¬СШBA·ҪПтТФ1cm/sөДЛЩ¶ИПтөгAФЛ¶ҜЈ®өұөгPөҪҙпөгBКұЈ¬PЈ¬QБҪөгН¬КұНЈЦ№ФЛ¶ҜЈ¬ТФAPОӘТ»ұЯПтЙПЧчХэ·ҪРОAPDEЈ¬№эөгQЧчQFЎОBCЈ¬Ҫ»ACУЪөгFЈ®ЙиөгPөДФЛ¶ҜКұјдОӘtsЈ¬Хэ·ҪРОәНМЭРОЦШәПІҝ·ЦөДГж»эОӘScm2Ј®
ЈЁ1Ј©өұt=ЎЎ_________ЎЎsКұЈ¬өгPУлөгQЦШәПЈ»
ЈЁ2Ј©өұt=ЎЎ_________ЎЎsКұЈ¬өгDФЪQFЙПЈ»
ЈЁ3Ј©өұөгPФЪQЈ¬BБҪөгЦ®јдЈЁІ»°ьАЁQЈ¬BБҪөгЈ©КұЈ¬ЗуSУлtЦ®јдөДәҜКэ№ШПөКҪЈ®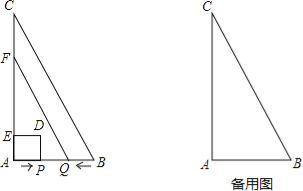
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ДіәУөМөДәб¶ПГжКЗМЭРОABCDЈ¬BCЎОADЈ¬BEЎНADУЪөгEЈ¬AB=50ГЧЈ¬BC=30ГЧЈ¬ЎПA=60ЎгЈ¬ЎПD=30ЎгЈ®ЗуADөДіӨ¶ИЈ®
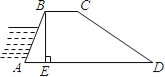
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘјНДоҪЁ№ъ70ЦЬДкЈ¬ДіРЈҫЩРР°ај¶ёиУҪұИИьЈ¬ёиЗъУРЈәЎ¶ОТ°®ДгЈ¬ЦР№ъЎ·Ј¬Ў¶ёиіӘЧж№ъЎ·Ј¬Ў¶ОТәНОТөДЧж№ъЎ·ЈЁ·ЦұрУГЧЦДёAЈ¬BЈ¬CТАҙОұнКҫХвИэКЧёиЗъЈ©Ј®ұИИьКұЈ¬Ҫ«AЈ¬BЈ¬CХвИэёцЧЦДё·ЦұрРҙФЪ3ХЕОЮІоұрІ»НёГчөДҝЁЖ¬ХэГжЙПЈ¬ПҙФИәуХэГжПтПВ·ЕФЪЧАГжЙПЈ¬°ЛЈЁ1Ј©°а°аіӨПИҙУЦРЛж»ъійИЎТ»ХЕҝЁЖ¬Ј¬·Е»ШәуПҙФИЈ¬ФЩУЙ°ЛЈЁ2Ј©°а°аіӨҙУЦРЛж»ъійИЎТ»ХЕҝЁЖ¬Ј¬ҪшРРёиУҪұИИьЈ®
ЈЁ1Ј©°ЛЈЁ1Ј©°аійЦРёиЗъЎ¶ОТәНОТөДЧж№ъЎ·өДёЕВККЗ__________Ј»
ЈЁ2Ј©КФУГ»ӯКчЧҙНј»тБРұнөД·Ҫ·ЁұнКҫЛщУРҝЙДЬөДҪб№ыЈ¬ІўЗуіц°ЛЈЁ1Ј©°аәН°ЛЈЁ2Ј©°аійЦРІ»Н¬ёиЗъөДёЕВКЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЕЧОпПЯ![]() ҝӘҝЪПтПВЈ¬Ул
ҝӘҝЪПтПВЈ¬Ул![]() ЦбҪ»УЪөг
ЦбҪ»УЪөг![]() Ј¬¶ҘөгЧшұкОӘ
Ј¬¶ҘөгЧшұкОӘ![]() Ј¬Ул
Ј¬Ул![]() ЦбөДҪ»өгФЪ
ЦбөДҪ»өгФЪ![]() Ј¬
Ј¬![]() Ц®јдЈЁ°ьә¬¶ЛөгЈ©Ј¬ФтПВБРҪбВЫЈә
Ц®јдЈЁ°ьә¬¶ЛөгЈ©Ј¬ФтПВБРҪбВЫЈә
ўЩ![]() Ј»ўЪ
Ј»ўЪ![]() Ј»ўЫ¶ФУЪИОТвКөКэ
Ј»ўЫ¶ФУЪИОТвКөКэ![]() Ј¬
Ј¬![]() ЧЬіЙБўЈ»
ЧЬіЙБўЈ»
ўЬ№ШУЪ![]() өД·ҪіМ
өД·ҪіМ![]() УРБҪёцІ»ПаөИөДКөКэёщ.
УРБҪёцІ»ПаөИөДКөКэёщ.
ЖдЦРҪбВЫХэИ·өДёцКэКЗЈЁ Ј©
A. 1ёцB. 2ёц
C. 3ёцD. 4ёц
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪГҝёцРЎХэ·ҪРОөДұЯіӨОӘ1өДНшёсЦРЈ¬өг![]() ¶јФЪёсөгЙПЎЈ
¶јФЪёсөгЙПЎЈ

ЈЁўсЈ©ACөДіӨКЗ_____________Ј»
ЈЁўтЈ©Ҫ«ЛДұЯРО![]() ХЫөюЈ¬К№өгCУлөг4ЦШәПЈ¬ХЫәЫEFҪ»BCУЪөгEЈ¬Ҫ»ADУЪөгFЈ¬өгDөД¶ФУҰөгОӘQЈ¬өГОеұЯРО
ХЫөюЈ¬К№өгCУлөг4ЦШәПЈ¬ХЫәЫEFҪ»BCУЪөгEЈ¬Ҫ»ADУЪөгFЈ¬өгDөД¶ФУҰөгОӘQЈ¬өГОеұЯРО![]() .ЗлУГОЮҝМ¶ИөДЦұіЯФЪНшёсЦР»ӯіцХЫөюәуөДОеұЯРОЈ¬ІўјтТӘЛөГчөг
.ЗлУГОЮҝМ¶ИөДЦұіЯФЪНшёсЦР»ӯіцХЫөюәуөДОеұЯРОЈ¬ІўјтТӘЛөГчөг![]() өДО»ЦГКЗИзәОХТөҪөД____________________.
өДО»ЦГКЗИзәОХТөҪөД____________________.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬AЈ¬BКЗ·ҙұИАэәҜКэyЈҪ![]() ЈЁxЈҫ0Ј©НјПуЙПөДБҪөгЈ¬·Цұр№эAЈ¬BБҪөгПтxЦбЈ¬yЦбЧчҙ№ПЯ¶ОЈ¬ADЈ¬BEБҪҙ№ПЯ¶ОҪ»УЪөгGЈ®ИфНјЦРТхУ°Іҝ·ЦөДГж»эОӘ3Ј¬ФтЎчOABөДГж»эОӘЈЁЎЎЎЎЈ©
ЈЁxЈҫ0Ј©НјПуЙПөДБҪөгЈ¬·Цұр№эAЈ¬BБҪөгПтxЦбЈ¬yЦбЧчҙ№ПЯ¶ОЈ¬ADЈ¬BEБҪҙ№ПЯ¶ОҪ»УЪөгGЈ®ИфНјЦРТхУ°Іҝ·ЦөДГж»эОӘ3Ј¬ФтЎчOABөДГж»эОӘЈЁЎЎЎЎЈ©
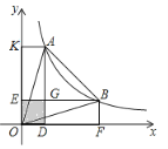
A.9B.10C.11D.12
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЦұПЯyЈҪx+mУлЛ«ЗъПЯyЈҪ![]() ПаҪ»УЪAЈЁ2Ј¬1Ј©Ј¬BБҪөгЈ®
ПаҪ»УЪAЈЁ2Ј¬1Ј©Ј¬BБҪөгЈ®
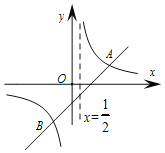
ЈЁ1Ј©ЗуіцТ»ҙОәҜКэУл·ҙұИАэәҜКэөДҪвОцКҪЈ¬ІўЗуіцBөгЧшұкЈ»
ЈЁ2Ј©ИфPОӘЦұПЯxЈҪ![]() ЙПТ»өгЈ¬өұЎчAPBөДГж»эОӘ6КұЈ¬ЗлЗуіцөгPөДЧшұкЈ®
ЙПТ»өгЈ¬өұЎчAPBөДГж»эОӘ6КұЈ¬ЗлЗуіцөгPөДЧшұкЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФД¶БПВБРІДБПЈ¬ҪвҙрОКМв
ЈЁ2x©Ғ5Ј©2+ЈЁ3x+7Ј©2=ЈЁ5x+2Ј©2
ҪвЈәЙиm=2x©Ғ5Ј¬n=3x+7Ј¬Фтm+n=5x+2
ФтФӯ·ҪіМҝЙ»ҜОӘm2+n2=ЈЁm+nЈ©2
ЛщТФmn=0Ј¬јҙЈЁ2x©Ғ5Ј©ЈЁ3x+7Ј©=0
ҪвЦ®өГЈ¬x1=![]() Ј¬x2=©Ғ
Ј¬x2=©Ғ![]()
ЗлАыУГЙПКц·Ҫ·ЁҪв·ҪіМЈЁ4x©Ғ5Ј©2+ЈЁ3x©Ғ2Ј©2=ЈЁx©Ғ3Ј©2
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com