
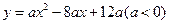 与
与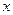 轴交于
轴交于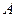 、
、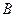 两点(点
两点(点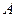 在点
在点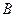 的左侧),抛物线上另有一点
的左侧),抛物线上另有一点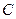 在第一象限,满足∠
在第一象限,满足∠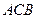 为直角,且恰使△
为直角,且恰使△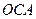 ∽△
∽△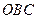 .
.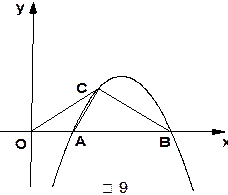
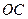 的长.
的长. 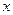 轴上是否存在点
轴上是否存在点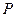 ,使△
,使△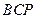 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的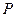 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由. 
 x
x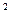 +
+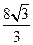 x-4
x-4
 ,0),(4,0),(6+2
,0),(4,0),(6+2 ,0)解析:
,0)解析: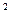 -8ax+12a=0(a<0)得
-8ax+12a=0(a<0)得 x
x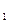 =2,x
=2,x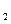 =6
=6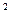 =OA·OB=2×6 ……2分
=OA·OB=2×6 ……2分  (-2
(-2 舍去)
舍去) ……3分
……3分 ∴
∴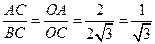
 k
k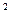 +BC
+BC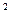 =AB
=AB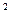 得
得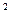 +(
+( k)
k)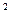 =(6-2)
=(6-2)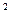
 =OC ……1分
=OC ……1分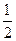 OB=3
OB=3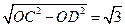
 ) ……2分
) ……2分 =a(3-2)(3-6)
=a(3-2)(3-6)
 x
x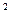 +
+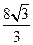 x-4
x-4 ……3分
……3分 与O重合时,△BCP
与O重合时,△BCP 为等腰三角形
为等腰三角形 的坐标为(0,0) ……1分
的坐标为(0,0) ……1分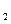 B=BC时(P
B=BC时(P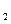 在B点的左侧),△BCP
在B点的左侧),△BCP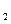 为等腰三角形
为等腰三角形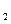 的坐标为(6-2
的坐标为(6-2 ,0) ……2分
,0) ……2分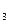 为AB的中点时,P
为AB的中点时,P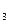 B=P
B=P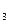 C,△BCP
C,△BCP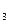 为等腰三角形
为等腰三角形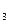 的坐标为(4,0) ……3分
的坐标为(4,0) ……3分 当BP
当BP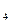 =BC时(P
=BC时(P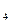 在B点的右侧),△BCP
在B点的右侧),△BCP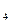 为等腰三角形
为等腰三角形 的坐标为(6+2
的坐标为(6+2 ,0)
,0)  ,0),(4,0),(6+2
,0),(4,0),(6+2 ,0) ……4分
,0) ……4分 

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
如图9,抛物线与
轴交于A、B两点,与
轴交于点C(0,
).
(1)求抛物线的对称轴及的值;
(2)抛物线的对称轴上存在一点P,使得的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
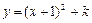 与
与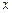 轴交于A、B两点,与
轴交于A、B两点,与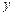 轴交于点C(0,
轴交于点C(0,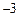 ).
).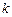 的值;
的值;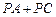 的值最小,求此时点P的坐标;
的值最小,求此时点P的坐标;
查看答案和解析>>
科目:初中数学 来源:2010-2011学年河北省石家庄市九年级第一次模拟考试数学 题型:解答题
如图9,抛物线 与
与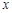 轴交于A、B两点,与
轴交于A、B两点,与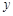 轴交于点C(0,
轴交于点C(0,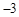 ).
).
(1)求抛物线的对称轴及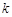 的值;
的值;
(2)抛物线的对称轴上存在一点P,使得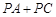 的值最小,求此时点P的坐标;
的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源:2010-2011学年江苏省常州市考模拟数学卷 题型:解答题
如图9,抛物线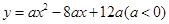 与
与 轴交于
轴交于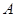 、
、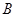 两点(点
两点(点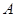 在点
在点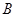 的左侧),抛物线上另有一点
的左侧),抛物线上另有一点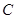 在第一象限,满足∠
在第一象限,满足∠ 为直角,且恰使△
为直角,且恰使△ ∽△
∽△ .
.
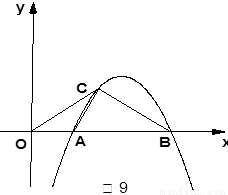
(1)(3分)求线段 的长.
的长.
(2)(3分)求该抛物线的函数关系式.
(3)(4分)在 轴上是否存在点
轴上是否存在点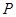 ,使△
,使△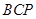 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的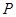 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com