
【题目】如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S、S1、S2 , 若S=2,则S1+S2=( )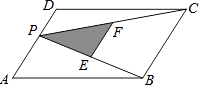
A.4
B.6
C.8
D.不能确定
【答案】C
【解析】解:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
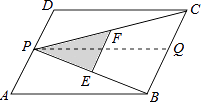
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,EF= ![]() BC,
BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S△PBC=1:4,S△PEF=2,
∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=8.
所以答案是:C.
【考点精析】认真审题,首先需要了解三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半),还要掌握平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】五一小长假的某一天,亮亮全家上午![]() 时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )

A.景点离亮亮的家![]() 千米
千米
B.亮亮到家的时间为![]() 时
时
C.小汽车返程的速度为![]() 千米/时
千米/时
D.![]() 时至
时至![]() 时,小汽车匀速行驶
时,小汽车匀速行驶
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校在推进新课改的过程中,开设的体育选修课有:A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
(1)请你求出该班的总人数,并补全频数分布直方图;
(2)该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人任选2人了解他们对体育选课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点![]() 与点E,点
与点E,点![]() 与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点![]() 与点E,点
与点E,点![]() 与点F的坐标,并说说对应点的坐标有哪些特征;
与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点![]() 与点
与点![]() 也是通过上述变换得到的对应点,求
也是通过上述变换得到的对应点,求![]() 、b的值
、b的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是线段AB上一点,AC和DG相交于点E.
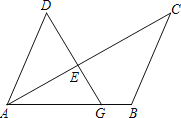
(1)请先作出∠ABC的平分线BF,交AC于点F;(尺规作图,保留作图痕迹,不写作法与证明)
(2)然后证明当:AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
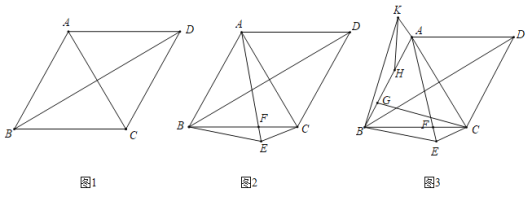
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)如下图,求证:四边形![]() 是菱形;
是菱形;
(2)如下图,点![]() 为四边形
为四边形![]() 外一点,连接
外一点,连接![]() 、
、![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)如下图,在(2)的条件下,![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 延长线上一点,
延长线上一点,![]() ,连接
,连接![]() ,
,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 的算术平方根是3,
的算术平方根是3,![]() 的立方根是-2.
的立方根是-2.
(1)求![]() 和
和![]() 的值.
的值.
(2)用四则运算的加、减、乘、除定义一个新运算:![]() .
.
①若![]() ,
,![]() 2
2![]() ,判断点P(-
,判断点P(-![]() ,-
,-![]() )在第几象限?
)在第几象限?
②若![]() 满足
满足![]() ,且3
,且3![]() ,化简
,化简![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
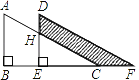
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com