
【题目】如图,小黄站在河岸上的![]() 点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船
点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船![]() 的俯角是
的俯角是![]() ,若小黄的眼睛与地面的距离
,若小黄的眼睛与地面的距离![]() 是
是![]() 米,
米,![]() 米,
米,![]() 平行于
平行于![]() 所在的直线,迎水坡
所在的直线,迎水坡![]() 的坡度为
的坡度为![]() ,坡长
,坡长![]() 米,则此时小船
米,则此时小船![]() 到岸边的距离
到岸边的距离![]() 的长为( )米.(
的长为( )米.(![]() ,结果保留两位有效数字)
,结果保留两位有效数字)
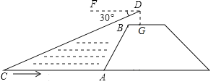
A. 11 B. 8.5 C. 7.2 D. 10
【答案】D
【解析】
把AB和CD都整理为直角三角形的斜边,利用坡度和勾股定理易得点B和点D到CA的距离,进而利用俯角的正切值可求得CH长度.CH﹣AE=EH即为AC长度.
过点B作BE⊥AC于点E,延长DG交CA于点H,得Rt△ABE和矩形BEHG.
∵i=![]() =
=![]() ,设BE=4x,则AE=3x,AB=5x.
,设BE=4x,则AE=3x,AB=5x.
∵AB=10.5,∴x=2.1,∴BE=8.4,AE=6.3.
∵DG=1.6,BG=0.7,∴DH=DG+GH=1.6+8.4=10,AH=AE+EH=6.3+0.7=7.
在Rt△CDH中,∵∠C=∠FDC=30°,DH=10,tan30°=![]() =
=![]() ,∴CH≈17.
,∴CH≈17.
又∵CH=CA+7,即17=CA+7,∴CA=17﹣7=10(米).
故选D.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
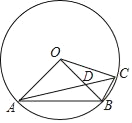
【题目】如图,⊙O是△ABC的外接圆,OA=2cm,OA⊥OB,AC交OB于D点,AD=2CD.
(1)求∠BOC的度数;
(2)求线段BD、线段CD和 BC围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
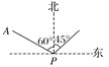
【题目】如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向.求货船的航行速度.(精确到0.1海里/时,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
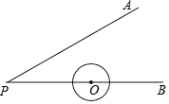
【题目】如图,已知∠APB=30°,OP=3cm,⊙O的半径为1cm,若圆心O沿着BP的方向在直线BP上移动.(1)当圆心O移动的距离为1cm时,则⊙O与直线PA的位置关系是_____.(2)若圆心O的移动距离是d,当⊙O与直线PA相交时,则d的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上运动(不与点
上运动(不与点![]() 重合).
重合).
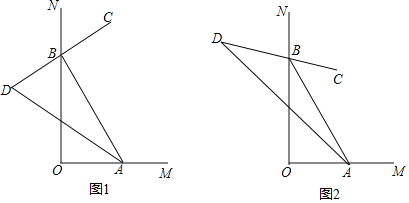
(1)如图1,![]() 是
是![]() 的平分线,
的平分线,![]() 的反方向延长线与
的反方向延长线与![]() 的平分线交于点
的平分线交于点![]() .
.
①若![]() ,则
,则![]() 为多少度?请说明理由.
为多少度?请说明理由.
②猜想:![]() 的度数是否随
的度数是否随![]() 、
、![]() 的移动发生变化?请说明理由.
的移动发生变化?请说明理由.
(2)如图2,若![]() ,
,![]() ,则
,则![]() 的大小为 度(直接写出结果);
的大小为 度(直接写出结果);
(3)若将“![]() ”改为“
”改为“![]() (
(![]() )”,且
)”,且![]() ,
,![]() ,其余条件不变,则
,其余条件不变,则![]() 的大小为 度(用含
的大小为 度(用含![]() 、
、![]() 的代数式直接表示出米).
的代数式直接表示出米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
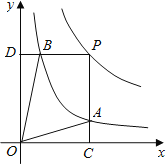
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com